题目内容
有四个函数:①y=sinx+cosx;②y=sinx-cosx;③y=(sinx+cosx)2;④y=sin2x-cos2x;其中在(0,
)上不是单调函数的是( )
| π |
| 2 |
| A、①和④ | B、②和③ |
| C、①和③ | D、②和④ |
分析:利用三角恒等变换公式,分别将各项中的函数化简为正弦型三角函数的形式,再根据正弦函数的单调性加以判断,可得只有①③的函数在(0,
)上不是单调函数,从而得到本题答案.
| π |
| 2 |
解答:解:对于①,y=sinx+cosx=
(sinxcos
+cosxsin
)=
sin(x+
),
∵当x∈(0,
)时,x+
∈(
,
),
∴函数y=sinx+cosx在(0,
)上为增函数,在(
,
)上为减函数,
故y=sinx+cosx在(0,
)上不是单调函数;
对于②,y=sinx+cosx=
(sinxcos
-cosxsin
)=
sin(x-
),
∵当x∈(0,
)时,x-
∈(-
,
),
∴函数y=sinx+cosx在(0,
)上为单调增函数;
对于③,y=(sinx+cosx)2=sin2x+2sinxcosx+cos2x=1+sin2x,
∵当x∈(0,
)时,2x∈(0,π),
∴函数y=(sinx+cosx)2在(0,
)上为增函数,在(
,
)上为减函数,
故y=(sinx+cosx)2在(0,
)上不是单调函数;
对于④,y=sin2x-cos2x=-cos2x=sin(2x-
),
∵当x∈(0,
)时,2x-
∈(-
,
),
∴函数y=(sinx+cosx)2在(0,
)上为单调增函数.
综上所述,只有①③的函数在(0,
)上不是单调函数.
故选:C
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∵当x∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴函数y=sinx+cosx在(0,
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故y=sinx+cosx在(0,
| π |
| 2 |
对于②,y=sinx+cosx=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 4 |
∵当x∈(0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∴函数y=sinx+cosx在(0,
| π |
| 2 |
对于③,y=(sinx+cosx)2=sin2x+2sinxcosx+cos2x=1+sin2x,
∵当x∈(0,
| π |
| 2 |
∴函数y=(sinx+cosx)2在(0,
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
故y=(sinx+cosx)2在(0,
| π |
| 2 |
对于④,y=sin2x-cos2x=-cos2x=sin(2x-
| π |
| 2 |
∵当x∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴函数y=(sinx+cosx)2在(0,
| π |
| 2 |
综上所述,只有①③的函数在(0,
| π |
| 2 |
故选:C
点评:本题给出几个三角函数表达式,求它在区间(0,
)上是否为单调函数.着重考查了三角恒等变换、正弦函数的图象与性质等知识,属于中档题.
| π |
| 2 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 -1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x).
-1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x).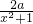 )+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.
)+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由. -1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x).
-1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x). )+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.
)+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.