题目内容
叙述两角差的余弦公式，并用向量的数量积证明．
两角差的余弦公式：cos（α-β）=cosαcosβ+sinαsinβ，证明如下：
以坐标原点为中心作单位圆，以Ox为始边作α、β，它们的终边分别与单位圆相交于点P，Q，则P（cosα，sinα），Q（cosβ，sinβ），|
|=|
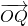|=1
∵α-β=
+2kπ，k∈Z（左图），或β-α=+2kπ，k∈Z（右图），
∴cos（α-β）=cos=
=
=（cosα，sinα）•（cosβ，sinβ）=cosαcosβ+sinαsinβ
分析：先写出两角差的余弦公式，再以坐标原点为中心作单位圆，以Ox为始边作α、β，它们的终边分别与单位圆相交于点P，Q，利用向量的数量积公式可得结论．
点评：本题考查两角差的余弦公式，考查向量的数量积，考查学生的计算能力，属于基础题．
以坐标原点为中心作单位圆，以Ox为始边作α、β，它们的终边分别与单位圆相交于点P，Q，则P（cosα，sinα），Q（cosβ，sinβ），|
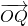|=||=1∵α-β=
+2kπ，k∈Z（左图），或β-α=+2kπ，k∈Z（右图），∴cos（α-β）=cos
===（cosα，sinα）•（cosβ，sinβ）=cosαcosβ+sinαsinβ分析：先写出两角差的余弦公式，再以坐标原点为中心作单位圆，以Ox为始边作α、β，它们的终边分别与单位圆相交于点P，Q，利用向量的数量积公式可得结论．
点评：本题考查两角差的余弦公式，考查向量的数量积，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目