题目内容

已知P是椭圆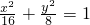 $数学公式$ 上任意一点，EF是圆M：x²+（y-2）²=1的直径，则 $数学公式$ 的最大值为________．

23
分析：根据题意可求得 $\text{[math]}$ = $\text{[math]}$ 进而将问题转化为求 $\text{[math]}$ 的最大值设P（x₀，y₀），代入椭圆的方程，根据点N的坐标表示出 $\text{[math]}$ 根据y₀的范围求得， $\text{[math]}$ 取最大值进而求得 $\text{[math]}$ 的最大值．
解答： $\text{[math]}$ = $\text{[math]}$
从而将求 $\text{[math]}$ 的最大值转化为求 $\text{[math]}$ 的最大值
是椭圆M上的任一点，设P（x₀，y₀），则有 $\text{[math]}$ 即x₀²=16-2y₀²
又M（0，2），所以 $\text{[math]}$
而y₀∈[-2 $\text{[math]}$ ，2 $\text{[math]}$ ]，所以当y₀=-2时， $\text{[math]}$ 取最大值24，
故 $\text{[math]}$ 的最大值为23．
故答案为：23．
点评：本题主要考查了直线与圆锥曲线的问题，向量的基本计算．考查了学生分析问题和解决问题的能力．

练习册系列答案

初中总复习优化设计系列答案

初中新课标名师学案智慧大课堂系列答案

高速课堂系列答案

资源与评价黑龙江教育出版社系列答案

课时全练讲练测达标100分系列答案

点金训练精讲巧练系列答案

火线100天中考滚动复习法系列答案

新课堂同步学习与探究系列答案

优等生单元期末冲刺100分系列答案

绿色指标自我提升系列答案

相关题目

已知椭圆C的中心在坐标原点，长轴在x轴上，F₁、F₂分别为其左、右焦点，P在椭圆上任意一点，且

的最大值为1，最小值为-2．
（1）求椭圆C的方程；
（2）设A为椭圆C的右顶点，直线l是与椭圆交于M、N两点的任意一条直线，若AM⊥AN，证明直线l过定点．

在平面直角坐标系xOy中，已知椭圆E：

=1（a＞b＞0）的离心率为

，一条准线方程为x=4．
（1）求椭圆E的标准方程；
（2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M，设直线OM的斜率为k₁，直线BP的斜率为k₂，求证：k₁k₂为定值．

（2013•深圳一模）已知椭圆C 的中心为原点O，焦点在x 轴上，离心率为

)在该椭圆上．
（1）求椭圆C的方程；
（2）如图，椭圆C 的长轴为AB，设 P 是椭圆上异于 A、B 的任意一点，PH⊥x轴，H为垂足，点Q 满足

，直线AQ与过点B 且垂直于x 轴的直线交于点M，

．求证：∠OQN为锐角．

已知圆O的半径为定长r，A是圆所在平面内一定点，P是圆上任意一点，线段AP的垂直平分线l与直线OP相交于点Q，当P在圆上运动时，点Q的轨迹可能是下列图形中的：

．（填写所有可能图形的序号）
①点；②直线；③圆；④抛物线；⑤椭圆；⑥双曲线；⑦双曲线的一支．

已知是椭圆的两焦点，P是椭圆上任意一点，过一焦点引的外角平分线的垂线，垂足为Q，则动点Q的轨迹为（ ▲ ）

A．圆 B．椭圆 C．双曲线 D．抛物线