题目内容
函数 的最大值为
的最大值为
- A.

- B.

- C.

- D.

C
分析:将函数y解析式第一项利用诱导公式化简,第二项利用两角和与差的余弦函数公式及特殊角的三角函数值化简,整理后,再利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域,即可得出y的最大值.
解答:y= sin(x+
sin(x+ )+cos(
)+cos( -x)
-x)
= cosx+
cosx+ cosx+
cosx+ sinx
sinx
= cosx+
cosx+ sinx
sinx
= (
( cosx+
cosx+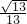 sinx)
sinx)
= sin(x+θ)(其中sinθ=
sin(x+θ)(其中sinθ= ,cosθ=
,cosθ=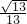 ),
),
∵-1≤sin(x+θ)≤1,
∴函数y的最大值为 .
.
故选C
点评:此题考查了两角和与差的正弦、余弦函数公式,正弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
分析:将函数y解析式第一项利用诱导公式化简,第二项利用两角和与差的余弦函数公式及特殊角的三角函数值化简,整理后,再利用两角和与差的正弦函数公式化为一个角的正弦函数,由正弦函数的值域,即可得出y的最大值.
解答:y=
 sin(x+
sin(x+ )+cos(
)+cos( -x)
-x)=
 cosx+
cosx+ cosx+
cosx+ sinx
sinx=
 cosx+
cosx+ sinx
sinx=
 (
( cosx+
cosx+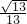 sinx)
sinx)=
 sin(x+θ)(其中sinθ=
sin(x+θ)(其中sinθ= ,cosθ=
,cosθ=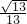 ),
),∵-1≤sin(x+θ)≤1,
∴函数y的最大值为
 .
.故选C
点评:此题考查了两角和与差的正弦、余弦函数公式,正弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
 ,
, 的最大值为
的最大值为 B.0 C.
B.0 C.  D.
D.

 ,
, 的最大值为
的最大值为 B.0 C.
B.0 C.  D.
D.

 满足条件
满足条件 目标函数
目标函数 的最小值为
的最小值为 ,则该目标函数
,则该目标函数 的最大值为( )
的最大值为( )
 B.
B.
 C.
C.
 D.
D.

 ,
, 的最大值为( )
的最大值为( ) B.
B. C.
C.  D.
D.

 ,
, 的最大值为
的最大值为 B.
B. C.
C.  D.
D.
