题目内容
设数列{an}的前n项和为Sn,点 均在直线
均在直线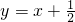 上.
上.
(1)求数列{an}的通项公式;
(2)设 ,试证明数列{bn}为等比数列.
,试证明数列{bn}为等比数列.
解:(1)∵点 均在直线
均在直线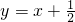 上,∴
上,∴ ,即
,即 .
.
∴当n≥2时,an=Sn-Sn-1= =2n-
=2n- .
.
当n=1时, =
= =
= ,即n=1时也成立.
,即n=1时也成立.
∴ (n∈N*).
(n∈N*).
(2)由(1)可得: ,
,
∴ =
= =32=9.
=32=9.
∴数列{bn}是以 =
= 为首项,9为公比的等比数列.
为首项,9为公比的等比数列.
分析:(1)利用公式 即可求出;
即可求出;
(2)利用(1)的结论和等比数列的定义即可证明.
点评:熟练掌握公式 和等比数列的定义是解题的关键.
和等比数列的定义是解题的关键.
 均在直线
均在直线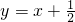 上,∴
上,∴ ,即
,即 .
.∴当n≥2时,an=Sn-Sn-1=
 =2n-
=2n- .
.当n=1时,
 =
= =
= ,即n=1时也成立.
,即n=1时也成立.∴
 (n∈N*).
(n∈N*).(2)由(1)可得:
 ,
,∴
 =
= =32=9.
=32=9.∴数列{bn}是以
 =
= 为首项,9为公比的等比数列.
为首项,9为公比的等比数列.分析:(1)利用公式
 即可求出;
即可求出;(2)利用(1)的结论和等比数列的定义即可证明.
点评:熟练掌握公式
 和等比数列的定义是解题的关键.
和等比数列的定义是解题的关键. 
练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目