题目内容
在△ABC中,cos2
=
=
,c=5,△ABC的内切圆的面积是______.
| A |
| 2 |
| b+c |
| 2c |
| 9 |
| 10 |
由cos2
=
,得cosA=
,又cos2
=
,所以cosA=
,再由余弦定理得b2+a2=c2,因为c=5,所以a=3,b=4.设其内切圆的半径为r,因为S=
(a+b+c)•r=
ab,∴r=1,所以内切圆的面积是π.
故答案为:π
| A |
| 2 |
| 9 |
| 10 |
| 4 |
| 5 |
| A |
| 2 |
| b+c |
| 2c |
| b |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:π

练习册系列答案
相关题目
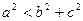 ,则角A的取值范围是 。
,则角A的取值范围是 。 中内角
中内角 的对边分别为
的对边分别为 ,若
,若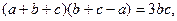 则角
则角