题目内容
已知定点A(-2,
),F是椭圆
+
=1的右焦点,在椭圆上求一点M,使|AM|+2|MF|取得最小值.
解：设点M(x,y),作MN垂直于椭圆的右准线l于N.
又椭圆的离心率e=,则2|MF|=|MN|,
|AM|+2|MF|=|AM|+|MN|,于是|AM|+2|MF|的最小值,即是|AM|+|MN|的最小值.
显然,当且仅当A、M、N三点共线(M在A、N之间)时,|AM|+|MN|最小,此时|AM|+2|MF|最小,
由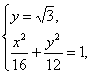得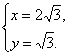
故所求点M的坐标为(2
,
).
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
)，点F为椭圆
=1的右焦点，点M的椭圆上移动时，求|AM|+2|MF|的最小值，并求此时点M的坐标.
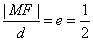
，设动点M的轨迹为曲线C.
与曲线C交于P,Q两点，若
，证明：
为定值.