题目内容
已知等比数列{an}公比q=2,其中a2,2a3+1,a5成等差数列,则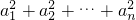 =
=
- A.

- B.

- C.
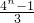
- D.

C
分析:根据题意,确定数列{an2}组成以1为首项,4为公比的等比数列,再利用求和公式,即可得到结论.
解答:∵等比数列{an}公比q=2,a2,2a3+1,a5成等差数列,
∴2(8a1+1)=2a1+16a1
∴a1=1
∴数列{an2}组成以1为首项,4为公比的等比数列
∴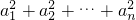 =
=
故选C.
点评:本题以等比数列为载体,考查等比数列的判定,考查等比数列的求和,属于基础题.
分析:根据题意,确定数列{an2}组成以1为首项,4为公比的等比数列,再利用求和公式,即可得到结论.
解答:∵等比数列{an}公比q=2,a2,2a3+1,a5成等差数列,
∴2(8a1+1)=2a1+16a1
∴a1=1
∴数列{an2}组成以1为首项,4为公比的等比数列
∴
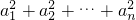 =
=
故选C.
点评:本题以等比数列为载体,考查等比数列的判定,考查等比数列的求和,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目