题目内容
在△ABC中, sin(
sin( -A)=3sin(π-A),且cosA=-
-A)=3sin(π-A),且cosA=- cos(π-B),则C等于( )
cos(π-B),则C等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
C
解析

练习册系列答案
相关题目
若函数 在
在 上单调递减,则
上单调递减,则 可以是( )
可以是( )
| A.1 | B. | C. | D. |
设sin( +θ)=
+θ)= ,则sin2θ等于( )
,则sin2θ等于( )
A.- | B. | C. | D. |
函数y=4sin(2x+ )的一个单调区间是 ( )
)的一个单调区间是 ( )
A.[ , , ] ] | B.[- , , ] ] |
C.[0, ] ] | D.[0, ] ] |
已知x∈(0, ),则函数f(x)=
),则函数f(x)= 的最大值为( )
的最大值为( )
| A.0 | B. | C. | D.1 |
已知sinx=2cosx,则sin2x+1=( )
A. | B. | C. | D. |
如图是函数y=Asin(ωx+φ) 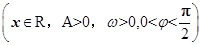 在区间
在区间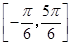 上的图像.为了得到这个函数的图像,只需将y=sin x(x∈R)的图像上所有的点( )
上的图像.为了得到这个函数的图像,只需将y=sin x(x∈R)的图像上所有的点( )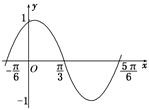
A.向左平移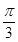 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的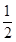 ,纵坐标不变 ,纵坐标不变 |
B.向左平移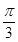 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移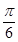 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的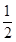 ,纵坐标不变 ,纵坐标不变 |
D.向左平移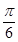 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
将函数y=sin 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为( ).
个单位,则所得函数图象对应的解析式为( ).
A.y=sin | B.y=sin |
C.y=sin x x | D.y=sin |
 .
.