Question

某加工厂用某原料由甲车间加工出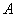产品，由乙车间加工出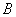产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克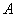产品，每千克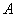产品获利50元.乙车间加工一箱原料需耗费工时6小时可加工出4千克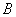产品，每千克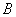产品获利60元.甲、乙两车间每天共能完成至多80箱原料的加工，每天甲、乙车间耗费工时总和不得超过600小时。

（1）若安排甲、乙两车间每天分别加工20箱和40箱原料，则甲、乙两车间每天共获利多少元？

（2）问应如何安排生产，才能使甲、乙两车间每天获利的总和最大？

Answer 1

（1）解：设获利的总和为Ｚ，则＝21400元

∴甲、乙两车间每天各加工40箱原料时，甲、乙两车间每天共获利21400元

（2）解：设应安排甲车间每天加工原料x箱，乙车间加工原料y箱，

则　　                                    

画出可行域如图　　　

目标函数z＝350x＋240y　

结合图象可得：当x＝30,y＝50时z最大为22500元

本题也可以将答案逐项代入检验.

答：安排甲车间加工原料30箱，乙车间加工原料50箱时，

甲、乙两车间每天获利的总和最大，为22500元。