题目内容
椭圆 ,过右焦点F且斜率为k(k>O)的直线与椭圆交于A,B两点,若
,过右焦点F且斜率为k(k>O)的直线与椭圆交于A,B两点,若 =3
=3 ,则k=
,则k=
- A.1
- B.

- C.

- D.2
B
分析:由椭圆的标准方程即可得到椭圆的右焦点F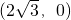 ,过右焦点F且斜率为k(k>O)的直线为
,过右焦点F且斜率为k(k>O)的直线为 ,其中
,其中 .与椭圆的方程联立消去x得到关于y的一元二次方程,利用根与系数的关系及若
.与椭圆的方程联立消去x得到关于y的一元二次方程,利用根与系数的关系及若 =3
=3 ,即可得到m,进而得到k.
,即可得到m,进而得到k.
解答:∵c2=a2-b2=16-4=12,∴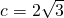 .
.
∴椭圆的右焦点F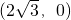 .
.
∴过右焦点F且斜率为k(k>O)的直线为 ,其中
,其中 .
.
设A(x1,y1),B(x2,y2).
联立 消去x得到
消去x得到 .
.
∴ ,
, .
.
∵ =3
=3 ,∴-y1=3y2,
,∴-y1=3y2,
把以上三式联立消去y1,y2,得到 =0,∴
=0,∴ ,即k2=2.
,即k2=2.
又∵k>0,∴k= .
.
故选B.
点评:熟练掌握椭圆的标准方程及其性质、把直线与椭圆相交问题转化为一元二次方程的根与系数的关系是解题的关键.
分析:由椭圆的标准方程即可得到椭圆的右焦点F
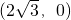 ,过右焦点F且斜率为k(k>O)的直线为
,过右焦点F且斜率为k(k>O)的直线为 ,其中
,其中 .与椭圆的方程联立消去x得到关于y的一元二次方程,利用根与系数的关系及若
.与椭圆的方程联立消去x得到关于y的一元二次方程,利用根与系数的关系及若 =3
=3 ,即可得到m,进而得到k.
,即可得到m,进而得到k.解答:∵c2=a2-b2=16-4=12,∴
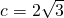 .
.∴椭圆的右焦点F
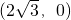 .
.∴过右焦点F且斜率为k(k>O)的直线为
 ,其中
,其中 .
.设A(x1,y1),B(x2,y2).
联立
 消去x得到
消去x得到 .
.∴
 ,
, .
.∵
 =3
=3 ,∴-y1=3y2,
,∴-y1=3y2,把以上三式联立消去y1,y2,得到
 =0,∴
=0,∴ ,即k2=2.
,即k2=2.又∵k>0,∴k=
 .
.故选B.
点评:熟练掌握椭圆的标准方程及其性质、把直线与椭圆相交问题转化为一元二次方程的根与系数的关系是解题的关键.

练习册系列答案
相关题目
 ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与C相交于A、B两点,若 = .
= . ,过右焦点F且斜率为k(k>O)的直线与椭圆交于A,B两点,若
,过右焦点F且斜率为k(k>O)的直线与椭圆交于A,B两点,若 =3
=3 ,则k=( )
,则k=( )
