Question

（本小题满分14分）

已知，函数.

(Ⅰ)当时，求使成立的的集合；

(Ⅱ)求函数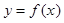在区间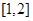上的最小值.

 

Answer 1

【答案】

(Ⅰ)  (Ⅱ)最小值为

【解析】

试题分析：（Ⅰ）由题意，.

当时，，解得或；

当时，，解得.

综上，所求解集为.

（Ⅱ）设此最小值为.

①当时，在区间上，.

因为，，

则在区间上是增函数，所以.

②当时，在区间上，，由知

.

③当时，在区间上，.

 .

若，在区间内，从而为区间上的增函数，

由此得.

若，则.

     当时，，从而为区间上的增函数；

     当时，，从而为区间上的减函数.

因此，当时，或.

当时，，故；

当时，，故.

综上所述，所求函数的最小值

考点：本小题主要考查含绝对值的函数的最值的求法和利用导数求函数的最值，考查学生分类讨论思想的应用和运算求解能力.

点评:求解含绝对值的不等式或函数问题，关键是通过讨论去掉绝对值符号，讨论的时候要注意做到“不重不漏”.