题目内容
如图,已知圆心坐标为 的圆
的圆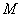 与
与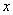 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为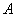 、
、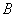 ,另一圆
,另一圆 与圆
与圆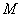 、
、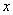 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为 、
、 .
.
(I)求圆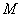 和圆
和圆 的方程;(II)过
的方程;(II)过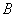 点作
点作 的平行线
的平行线 ,求直线
,求直线 被圆
被圆 截得的弦的长度.
截得的弦的长度.


【答案】解: (1)由于圆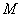 与
与 的两边相切,故
的两边相切,故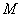 到
到 及
及 的距离均为圆
的距离均为圆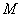 的半径,
的半径,
则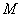 在
在  的角平分线上,同理,
的角平分线上,同理, 也在
也在 的角平分线上,
的角平分线上,
即 三点共线,且
三点共线,且 为
为 的角平分线,
的角平分线,

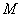 的坐标为
的坐标为 ,
, 到
到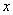 轴的距离为1,即:圆
轴的距离为1,即:圆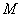 的半径为1,
的半径为1,
 圆
圆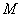 的方程为
的方程为 ;
;
设圆 的半径为
的半径为 ,由
,由 ,得:
,得: ,
,
即 ,
, ,
,  圆
圆 的方程为:
的方程为: ;
;
(2)由对称性可知,所求弦长等于过 点的
点的 的平行线被圆
的平行线被圆 截得的弦长,
截得的弦长,
此弦所在直线方程为 ,即
,即 ,
,
圆心 到该直线的距离
到该直线的距离 , 则弦长=
, 则弦长=

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 上一动点M,设M到抛物线C外一定点A(6,12)的距离为
上一动点M,设M到抛物线C外一定点A(6,12)的距离为 ,M到定直线
,M到定直线 的距离为
的距离为 ,若
,若 ,960分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷
,960分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷 ,编号落入区间[451,750]的人做问卷
,编号落入区间[451,750]的人做问卷 ,其余的人做问卷
,其余的人做问卷 .则抽到的人中,做问卷
.则抽到的人中,做问卷 B.
B. C.
C. D.
D.
 ,
, 的值为 ( )
的值为 ( )
 个单位长度,再把所得各点的横坐
个单位长度,再把所得各点的横坐 )
) x-
x- )
)
 的图像关于直线
的图像关于直线 对称,它的周期是
对称,它的周期是 ,则 ( )
,则 ( )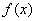 的图象过点
的图象过点 B.
B.  上是减函数
上是减函数  D.
D. 
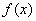 =
=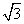
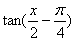 ,
,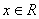 的最小正周期为
的最小正周期为 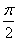 B.
B.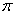 C.
C. D.
D.