题目内容
在样本的频率分布直方图中,一共有n个小矩形,若中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的 ,且样本容量为240,则中间一组的频数是
,且样本容量为240,则中间一组的频数是
- A.32
- B.30
- C.40
- D.60
C
分析:根据中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的 ,设出中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,得到中间一个的频率的值,用概率乘以样本容量得到结果.
,设出中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,得到中间一个的频率的值,用概率乘以样本容量得到结果.
解答:∵分类分步直方图共有n个小矩形,
中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的 ,
,
设中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,
∵x+5x=1,
∴x=
∵样本容量为240,
∴中间一组的频数是240× =40,
=40,
故选C.
点评:本题考查频率分布表,考查频率分步直方图小正方形的面积等于这组数据的频率,注意小正方形的面积之间的关系不要弄混,本题是一个基础题.
分析:根据中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的
 ,设出中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,得到中间一个的频率的值,用概率乘以样本容量得到结果.
,设出中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,得到中间一个的频率的值,用概率乘以样本容量得到结果.解答:∵分类分步直方图共有n个小矩形,
中间一个小矩形的面积等于其余(n-1)个小矩形面积之和的
 ,
,设中间一个小矩形的面积是x,则其余(n-1)个小矩形面积之和为5x,
∵x+5x=1,
∴x=

∵样本容量为240,
∴中间一组的频数是240×
 =40,
=40,故选C.
点评:本题考查频率分布表,考查频率分步直方图小正方形的面积等于这组数据的频率,注意小正方形的面积之间的关系不要弄混,本题是一个基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
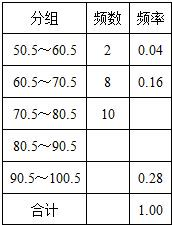 青少年“心理健康”问题已引起了全社会的关注,学校对此问题极为重视、对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正数,满分100分)作为样本,绘制了下面尚为完成的频率分布直方表.
青少年“心理健康”问题已引起了全社会的关注,学校对此问题极为重视、对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正数,满分100分)作为样本,绘制了下面尚为完成的频率分布直方表.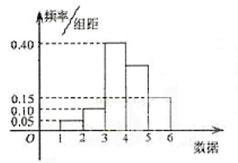 某个容量为N的样本的频率分布直方如图,现采用分层抽样的方法从区间[2,3]、[3,4]、[4,5]上抽取80个样本作进一步检测,已知在区间[4,5)上抽取的样本个数为30,则N=
某个容量为N的样本的频率分布直方如图,现采用分层抽样的方法从区间[2,3]、[3,4]、[4,5]上抽取80个样本作进一步检测,已知在区间[4,5)上抽取的样本个数为30,则N= 青少年“心理健康”问题已引起了全社会的关注,学校对此问题极为重视、对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正数,满分100分)作为样本,绘制了下面尚为完成的频率分布直方表.
青少年“心理健康”问题已引起了全社会的关注,学校对此问题极为重视、对全校600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正数,满分100分)作为样本,绘制了下面尚为完成的频率分布直方表.
