题目内容
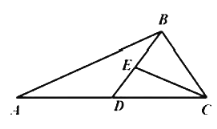
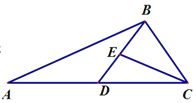
【题目】如图,在![]() 中,
中,![]() ,且D为
,且D为![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若![]() ,
,![]() ,
,![]() 的角平分线
的角平分线![]() 交
交![]() 于E,求
于E,求![]() 及
及![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]() ,
,![]()
【解析】
(1)由D为AC的中点,可得S△ABC=2S△BCD,进而利用三角形的面积公式即可求解![]() 的值.
的值.
(2)设BD=x,则AB=2x,在△ABC,△BCD中,利用余弦定理可得![]() ,解得x2
,解得x2![]() ,可求cos∠DCB的值,利用角平分线的性质可求
,可求cos∠DCB的值,利用角平分线的性质可求![]() ,可得S△CED
,可得S△CED![]() S△BCD,利用三角形的面积公式求得S△BCD的值,即可求解S△CED的值.
S△BCD,利用三角形的面积公式求得S△BCD的值,即可求解S△CED的值.
解:(1)∵S△ABC![]() ABBCsin∠ABC,S△BCD
ABBCsin∠ABC,S△BCD![]() BDBCsin∠DBC,
BDBCsin∠DBC,
∵D为AC的中点,
∴S△ABC=2S△BCD,即![]() ABBCsin∠ABC=2
ABBCsin∠ABC=2![]() BDBCsin∠DBC,
BDBCsin∠DBC,
∵sin∠ABC=sin∠DBC,
∴![]() .
.
(2)设BD=x,则AB=2x,
在△ABC中,cos∠ACB![]() ,
,
在△BCD中,cos∠DCB![]() ,
,
∴![]() ,解得x2
,解得x2![]() ,则cos∠DCB
,则cos∠DCB![]() ,
,
∵∠ACB的角平分线为CE,
∴E到DC,BC的距离相等,则![]() ,
,
∴S△CED![]() S△BCD,
S△BCD,
∴S△BCD![]() BCDCsin∠DCB
BCDCsin∠DCB![]() 4
4![]() ,
,
∴S△CED![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目