题目内容
已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q,且OP⊥OQ,|PQ|=![]() .求椭圆的方程.
.求椭圆的方程.
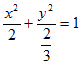 , 或
, 或 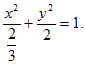
解析:
本小题考查椭圆的性质、两点的距离公式、两条直线垂直条件、二次方程根与系数的关系及分析问题的能力.满分12分.
解:求椭圆方程为![]()
依题意知,点P、Q的坐标满足方程组
|
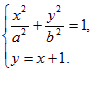
将②式代入①式,整理得(a2+b2)x2+2a2x+a2(1-b2)=0, ③ ——2分
设方程③的两个根分别为x1,x2,那么直线y=x+1与椭圆的交点为
P(x1,x1+1),Q(x2,x2+1). ——3分
由题设OP⊥OQ,|PQ|=![]() ,可得
,可得
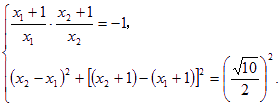
整理得
|
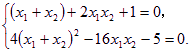 ——6分
——6分 解这个方程组,得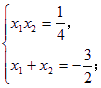 或
或 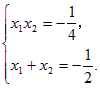
根据根与系数的关系,由③式得
(Ⅰ)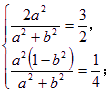 或 (Ⅱ)
或 (Ⅱ) 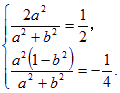 ——10分
——10分
解方程组(Ⅰ),(Ⅱ),得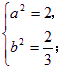 或
或 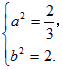
故所求椭圆的方程为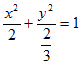 , 或
, 或 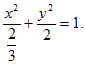 ——12分
——12分

练习册系列答案
相关题目
 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.