题目内容
给出四个命题:
①存在一个△ABC,使得sinA+cosA=-1;
②△ABC中,∠A>∠B的充要条件为sinA>sinB;
③直线x=
是函数y=sin(2x+
π)图象的一条对称轴;
④若关于x方程9x+(a+4)•3x+4=0有解,则实数a的取值范围为a≥0或a≤-8.
正确的个数为( )
①存在一个△ABC,使得sinA+cosA=-1;
②△ABC中,∠A>∠B的充要条件为sinA>sinB;
③直线x=
| π |
| 8 |
| 5 |
| 4 |
④若关于x方程9x+(a+4)•3x+4=0有解,则实数a的取值范围为a≥0或a≤-8.
正确的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
①△ABC中,若sinA+cosA=-1,两边同时平方可得1+2sinAcosA=1
∴sinAcosA=0
若sinA=0,则cosA=-1,A 不存在;若cosA=0,则sinA=-1,A不存在故①错误
②由A>B.三角形的大边对大角可得a>b,再由正弦定理可得,2RsinA>2RsinB,即sinA>sinB,反之也成立,故②正确
③由于函数y=sin(2x+
)的对称轴为:2x+
=kπ+
,即x=
kπ-
,令k=0可得函数的一条对称轴为x=
,故③正确
④若关于x方程9x+(a+4)•3x+4=0有解,(令t=3x>0),则t2+(a+3)t+4=0有大于0的根
则
∴
则实数a的取值范围为a≤-8.故④错误
故选:B
∴sinAcosA=0
若sinA=0,则cosA=-1,A 不存在;若cosA=0,则sinA=-1,A不存在故①错误
②由A>B.三角形的大边对大角可得a>b,再由正弦定理可得,2RsinA>2RsinB,即sinA>sinB,反之也成立,故②正确
③由于函数y=sin(2x+
| 5π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
④若关于x方程9x+(a+4)•3x+4=0有解,(令t=3x>0),则t2+(a+3)t+4=0有大于0的根
则
|
|
则实数a的取值范围为a≤-8.故④错误
故选:B

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
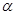 ,使
,使 ;②存在实数
;②存在实数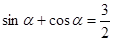 ;③
;③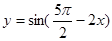 是偶函数;④
是偶函数;④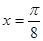 是函数
是函数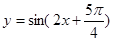 的一条对称轴方程;⑤若
的一条对称轴方程;⑤若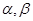 是第一象限角,且
是第一象限角,且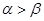 ,则
,则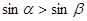 。其中所有的正确命题的序号是___ _.
。其中所有的正确命题的序号是___ _.