题目内容
已知f（x）是定义在R上不恒为零的函数，对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）成立． 数列{an}满足an=f（2n）（n∈N*），且a1=2．则数列的通项公式an=________．
n2n
分析：可根据an=f（2n）再利用对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）成立令x=2n，y=2得到递推关系式an+1=2an+2×2n然后两边同除以2n+1可构造出数列{
}是以
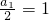为首项公差为1的等差数列后就可解决问题了．
解答：由于an=f（2n）则an+1=f（2n+1）且a1=2=f（2）
∵对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）
∴令x=2n，y=2则f（2n+1）=2nf（2）+2f（2n）
∴an+1=2an+2×2n
∴
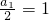∴数列{}是以为首项公差为1的等差数列
∴
∴an=n2n
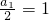点评：此题主要考查了利用函数的特征求数列的通项公式，是函数与数列的综合题．解题的关键是分别赋予x=2n，y=2得到an+1=2an+2×2n然后构造出数列{}是以为首项公差为1的等差数列后就可求解．同时要对递推关系式an+1=pan+qn通过两边同除以qn+1构造出{
}为等差数列进而求出an的通项公式．
分析：可根据an=f（2n）再利用对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）成立令x=2n，y=2得到递推关系式an+1=2an+2×2n然后两边同除以2n+1可构造出数列{
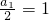}是以为首项公差为1的等差数列后就可解决问题了．解答：由于an=f（2n）则an+1=f（2n+1）且a1=2=f（2）
∵对于任意的x，y∈R，都有f（x•y）=xf（y）+yf（x）
∴令x=2n，y=2则f（2n+1）=2nf（2）+2f（2n）
∴an+1=2an+2×2n
∴
∴数列{
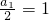}是以为首项公差为1的等差数列∴
∴an=n2n
点评：此题主要考查了利用函数的特征求数列的通项公式，是函数与数列的综合题．解题的关键是分别赋予x=2n，y=2得到an+1=2an+2×2n然后构造出数列{
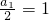}是以为首项公差为1的等差数列后就可求解．同时要对递推关系式an+1=pan+qn通过两边同除以qn+1构造出{}为等差数列进而求出an的通项公式． 
练习册系列答案
相关题目