题目内容
已知圆C：x2+y2=1，点A（-2，0）及点B（3，a），从A点观察B点，要使视线不被圆C挡住，则实数a的取值范围是
- A.
- B.
- C.
- D.y=kx-1
A
分析：先设过A的直线方程为：kx-y+2k=0，根据“使视线不被圆C挡住”则找到直线与圆相切的位置，这样，先求得圆心到直线的距离，再让其等于半径，求得直线方程，再令x=3得y=
，从而求得实数a的取值范围．
解答：
解：设过A的直线方程为：kx-y+2k=0
圆心到直线的距离为：
∵直线与圆相切
∴
∴k=
∴切线方程为：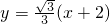
令x=3得：y=
∴使视线不被圆C挡住，则实数a的取值范围是，
故选A
点评：本题主要考查直线与圆的位置关系，作为相切是研究相交和相离的关键位置，应熟练掌握．
分析：先设过A的直线方程为：kx-y+2k=0，根据“使视线不被圆C挡住”则找到直线与圆相切的位置，这样，先求得圆心到直线的距离，再让其等于半径，求得直线方程，再令x=3得y=
，从而求得实数a的取值范围．解答：
解：设过A的直线方程为：kx-y+2k=0圆心到直线的距离为：
∵直线与圆相切
∴
∴k=
∴切线方程为：
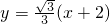
令x=3得：y=
∴使视线不被圆C挡住，则实数a的取值范围是
，故选A
点评：本题主要考查直线与圆的位置关系，作为相切是研究相交和相离的关键位置，应熟练掌握．
练习册系列答案
相关题目
（2009•普陀区一模）如图，已知圆C：x2+y2=r2与x轴负半轴的交点为A．由点A出发的射线l的斜率为k，且k为有理数．射线l与圆C相交于另一点B．