题目内容
已知函数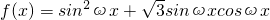 ,x∈R,又
,x∈R,又 ,若|α-β|的最小值为
,若|α-β|的最小值为 ,则正数ω的值为
,则正数ω的值为
- A.2
- B.1
- C.

- D.

D
分析:先利用二倍角公式和两角和公式对函数解析式化简整理,进而f(α),f(β)求得2ωα- 和2ωβ-
和2ωβ- ,进而二者相减求得2ωα-2ωβ 的表达式,进而根据|α-β|的最小值为
,进而二者相减求得2ωα-2ωβ 的表达式,进而根据|α-β|的最小值为 代入,根据ω为正整数,则可取k1=k2=1,求得答案.
代入,根据ω为正整数,则可取k1=k2=1,求得答案.
解答: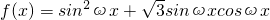
= -
- cos2ωx+
cos2ωx+ sin2ωx
sin2ωx
=cos(2ωx- )+
)+
f(α)=-
∴cos(2ωα- )=-1;
)=-1;
∴2ωα- =(2k1+1)π;
=(2k1+1)π;
∵f(β)=
∴cos(2ωβ- )=0;
)=0;
∴2ωβ- =k2π+
=k2π+ ;
;
∴2ωα-2ωβ=(2k1-k2)π+ ;
;
∴2ω•|α-β|=(2k1-k2) π+ ;
;
∵|α-β|≥ ,则
,则
∴2ω≤ [(2k1-k2)π+
[(2k1-k2)π+ ]=
]= [4(2k1-k2)+2]
[4(2k1-k2)+2]
ω≤ [2(2k1-k2)+1]
[2(2k1-k2)+1]
取k1=k2=1,
则可知ω=
故选D.
点评:本题主要考查了两角和公式和二倍角公式的化简求值.考查了学生综合分析问题和基本的运算能力.
分析:先利用二倍角公式和两角和公式对函数解析式化简整理,进而f(α),f(β)求得2ωα-
 和2ωβ-
和2ωβ- ,进而二者相减求得2ωα-2ωβ 的表达式,进而根据|α-β|的最小值为
,进而二者相减求得2ωα-2ωβ 的表达式,进而根据|α-β|的最小值为 代入,根据ω为正整数,则可取k1=k2=1,求得答案.
代入,根据ω为正整数,则可取k1=k2=1,求得答案.解答:
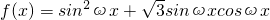
=
 -
- cos2ωx+
cos2ωx+ sin2ωx
sin2ωx=cos(2ωx-
 )+
)+
f(α)=-

∴cos(2ωα-
 )=-1;
)=-1;∴2ωα-
 =(2k1+1)π;
=(2k1+1)π;∵f(β)=

∴cos(2ωβ-
 )=0;
)=0;∴2ωβ-
 =k2π+
=k2π+ ;
;∴2ωα-2ωβ=(2k1-k2)π+
 ;
;∴2ω•|α-β|=(2k1-k2) π+
 ;
;∵|α-β|≥
 ,则
,则∴2ω≤
 [(2k1-k2)π+
[(2k1-k2)π+ ]=
]= [4(2k1-k2)+2]
[4(2k1-k2)+2]ω≤
 [2(2k1-k2)+1]
[2(2k1-k2)+1]取k1=k2=1,
则可知ω=

故选D.
点评:本题主要考查了两角和公式和二倍角公式的化简求值.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目
 ,x∈R,又
,x∈R,又 ,若|α-β|的最小值为
,若|α-β|的最小值为 ,则正数ω的值为( )
,则正数ω的值为( )

 ,x∈R,又
,x∈R,又 ,若|α-β|的最小值为
,若|α-β|的最小值为 ,则正数ω的值为( )
,则正数ω的值为( )

 ,x∈R,又
,x∈R,又 ,若|α-β|的最小值为
,若|α-β|的最小值为 ,则正数ω的值为( )
,则正数ω的值为( )
