题目内容
已知函数![]() ,
,![]()
(1)判断曲线![]() 在点(1,
在点(1,![]() )处的切线与曲线
)处的切线与曲线![]() 的公共点个数;
的公共点个数;
(2)若函数![]() 有且仅有一个零点,求
有且仅有一个零点,求![]() 的值;
的值;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围
的取值范围
(1)由已知得曲线在点(1,![]() )处的切线方程为
)处的切线方程为![]() (1分)
(1分)
代入![]() 得
得![]()
所以,当![]() 或
或![]() 时,有两个公共点;当
时,有两个公共点;当![]() 或
或![]() 时,有一个公共点;
时,有一个公共点;
当![]() 时,没有公共点 (4分)
时,没有公共点 (4分)
(2)![]() =
=![]() ,由
,由![]() 得
得![]() (5分)
(5分)
令![]() ,
,![]()
![]() (6分)
(6分)
所以,![]() 在(0,1)上递减,在(1,+∞)上递增 (7分)
在(0,1)上递减,在(1,+∞)上递增 (7分)
因此,![]()
![]()
![]() (8分)
(8分)
(3)![]() =
=![]() ,令
,令![]() =
=![]()
∴ ![]() ,即
,即![]() 有两个不同的零点
有两个不同的零点![]() ,(10分)
,(10分)
令![]() =
=![]()
![]()
![]()
![]()
![]() 且当
且当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,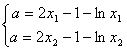
![]()
![]()
所以,![]() ,此时
,此时![]() (13分)
(13分)
即![]() 时,
时,![]()

练习册系列答案
相关题目

 (理)已知函数
(理)已知函数
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
 (理)已知函数
(理)已知函数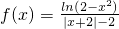 .
.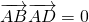 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
