题目内容
设等比数列 的前
的前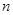 项和为
项和为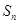 ,且
,且 ,
, ,则
,则 ( )
( )
| A.60 | B.70 | C.90 | D.40 |
B
解析试题分析:根据等比数列的性质可知 仍成等比数列,故
仍成等比数列,故 ,即
,即 ,解得
,解得 。故B正确。法二:还可由已知
。故B正确。法二:还可由已知 ,
, ,可得关于首项
,可得关于首项 和公比
和公比 的二元一次方程组,求首项
的二元一次方程组,求首项 和公比
和公比 ,再根据等比数列的前
,再根据等比数列的前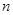 项和公式求
项和公式求 。故B正确。
。故B正确。
考点:1等比数列的性质;2等比数列的前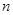 项和公式。
项和公式。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
等比数列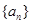 中,
中,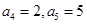 ,则数列
,则数列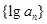 的前8项和等于( )
的前8项和等于( )
| A.6 | B.5 | C.4 | D.3 |
一无穷等比数列 各项的和为
各项的和为 ,第二项为
,第二项为 ,则该数列的公比为 ( )
,则该数列的公比为 ( )
A. . . | B. . . | C. . . | D. 或 或 . . |
已知等比数列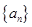 的公比为2,前4项的和是1,则前8项的和为( )
的公比为2,前4项的和是1,则前8项的和为( )
| A.23 | B.21 | C.19 | D.17 |
已知数列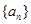 的通项
的通项 ,则
,则 ()
()
| A.0 | B. | C. | D. |
各项都是正数的等比数列{an}的公比q≠1且a2,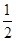 a3,a1成等差数列,则
a3,a1成等差数列,则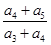 =( )
=( )
A.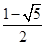 | B.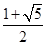 |
C.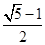 | D.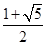 或 或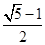 |
已知各项为正的等比数列{an}中,a4与a14的等比中项为2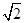 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )
| A.16 | B.8 | C.6 | D.4 |
[2014·北京西城区期末]设f(n)=2+24+27+210+…+23n+10(n∈N*),则f(n)等于( )
A. (8n-1) (8n-1) | B. (8n+1-1) (8n+1-1) |
C. (8n+3-1) (8n+3-1) | D. (8n+4-1) (8n+4-1) |
已知各项为正的等比数列{an}中,a4与a14的等比中项为 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )
| A.16 | B.8 | C. | D.4 |