��Ŀ����
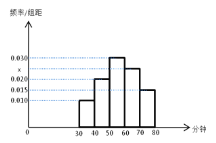
����Ŀ��4��23�������������������ij��ѧ�ڴ��ڼ俪չ��һϵ�еĶ���������Ϊ�˽ⱾУѧ�������Ķ������ѧУ�����ȡ��100��ѧ����������Ķ�ʱ����е��飬��ͼ�Ǹ��ݵ��������Ƶ�ѧ���վ������Ķ�ʱ��(��λ:����)��Ƶ�ʷֲ�ֱ��ͼ�������վ������Ķ�ʱ�䲻����60���ӵ�ѧ����Ϊ����������������60���ӵ�ѧ����Ϊ���Ƕ�������.
��1����![]() ��ֵ������ȫУ3000��ѧ���ж����մ���ж�����?����Ƶ����Ϊ���ʣ�
��ֵ������ȫУ3000��ѧ���ж����մ���ж�����?����Ƶ����Ϊ���ʣ�
��2��������֪�����������![]() �������������ݴ��ж��Ƿ���
�������������ݴ��ж��Ƿ���![]() �İ�����Ϊ�������������Ա��й�?
�İ�����Ϊ�������������Ա��й�?
�Ƕ����� | ������ | �ϼ� | |
�� | 40 | ||
Ů | 25 | ||
�ϼ� |
��: ��
��![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡���1��![]() ��3000��ѧ���ж����Դ����1200�ˣ�2�����������������а���
��3000��ѧ���ж����Դ����1200�ˣ�2�����������������а���
��������
��1������Ƶ�ʷֲ�ֱ��ͼ�����о��������Ϊ1�ɼ����![]() ���������ʱ��60�������ϵ�Ƶ�ʺ�ɵ�������
���������ʱ��60�������ϵ�Ƶ�ʺ�ɵ�������
��2������Ƶ�ʷֲ�ֱ��ͼ�����������������������ݹ�ʽ����![]() ��ɵý��ۣ�
��ɵý��ۣ�
��1������֪�ɵ�:![]() ���ɵ�
���ɵ�![]() ����Ϊ
����Ϊ![]() ����Ƶ����Ϊ���ʣ��ɴ˿��Թ����ȫУ3000��ѧ���ж����Դ����1200�ˣ�
����Ƶ����Ϊ���ʣ��ɴ˿��Թ����ȫУ3000��ѧ���ж����Դ����1200�ˣ�
��2����������![]() ����������
����������
�Ƕ����� | ������ | �ϼ� | |
�� | 40 | 15 | 55 |
Ů | 20 | 25 | 45 |
�ϼ� | 60 | 40 | 100 |
![]() ��
�� ![]() ������
������![]() �İ�����Ϊ�������������Ա��й�.
�İ�����Ϊ�������������Ա��й�.

 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�