题目内容

（2011•顺义区二模）设集合M={x|x2-1＜0}，N={x|2x＞1}，则M∪N等于（　　）
分析：把集合M和集合N的所有元素合并到一起，构成M∪N，由此利用集合M={x|x2-1＜0}={x|-1＜x＜1}，N={x|2x＞1}={x|x＞0}，能求出M∪N．
解答：解：∵集合M={x|x2-1＜0}={x|-1＜x＜1}，
N={x|2x＞1}={x|x＞0}，
M∪N={x|x＞-1}．
故选A．
点评：本题考查集合的并集的定义和运算，是基础题．解题时要认真审题，注意一元二次不等式和指数函数的性质的灵活运用．
练习册系列答案
相关题目
（2011•顺义区二模）在△ABC中，若b=1，c=
3
，∠A=
π
6
，则a=
1
1
．
（2011•顺义区二模）已知函数f(x)=2-sin(2x+
π
6
)-2sin2x，x∈R
（1）求函数f（x）的最小正周期；
（2）记△ABC的内角A，B，C的对边长分别为a，b，c，若f(
B
2
)=1，b=1，c=
3
，求a的值．
（2011•顺义区二模）已知定义在区间[0，
3π
2
]上的函数y=f（x）的图象关于直线x=
3π
4
对称，当x≥
3π
4
时，f（x）=cosx，如果关于x的方程f（x）=a有解，记所有解的和为S，则S不可能为（　　）
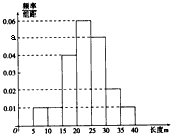（2011•顺义区二模）某棉纺厂为了解一批棉花的质量，从中随机抽测100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标）．所得数据均在区间[5，40]中，其频率分布直方图如图所示，由图中数据可知a=
0.05
0.05
，在抽测的100根中，棉花纤维的长度在[20，30]内的有
55
55
根．
（2011•顺义区二模）已知
e1
=(1，0)，
e2
=(0，1)，
a
=2
e1
+
e2
，
b
=λ
e1
-
e2
，当
a
∥
b
时，实数λ等于（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网