题目内容
设x、y、z∈R+且3x=4y=6z(1)求使2x=py的p的值 (2)求与(1)中所求P的差最小的整数
(3)求证:
| 1 |
| z |
| 1 |
| x |
| 1 |
| 2y |
分析:(1)可令3x=4y=6z=k,利用指对数互化,对数的运算性质解答.
(2)判断P的取值范围,找出与它最接近的2个整数,计算P与这2个整数的差.
(3)计算等式的左边和右边的值相等,等式得到证明.
(4)这3个数都是正数,比较它们的倒数的大小,从而得到这3个数大小关系.
(2)判断P的取值范围,找出与它最接近的2个整数,计算P与这2个整数的差.
(3)计算等式的左边和右边的值相等,等式得到证明.
(4)这3个数都是正数,比较它们的倒数的大小,从而得到这3个数大小关系.
解答:解:(1)令3x=4y=6z=k,则 x=log3k,y=log4k,z=log6k,∵2x=py,
∴2log3k=plog4k,∴P=
=2
=2log34.
(2)∵2log34=log316,2<log316<3,即 2<p<3,
∵P-2=
,3-P=
,
>
,∴P-2>3-P,
与P的差最小的整数是3.
(3)∵
-
=logk6-logk3=logk2,
=
•logk4=logk2,
∴
-
=
.
(4)3x=3log3k,4y=4log4k、6z=6log6k,又x、y、z∈R+,∴k>1,
∵
-
=
-
=
>0,∴3x<4y,
同理可求,
-
=
>0,∴4y<6z,∴3x<4y<6z
∴2log3k=plog4k,∴P=
2
| ||
|
| lg4 |
| lg3 |
(2)∵2log34=log316,2<log316<3,即 2<p<3,
∵P-2=
| log |
3 |
| log |
3 |
| 16 |
| 9 |
| 27 |
| 16 |
与P的差最小的整数是3.
(3)∵
| 1 |
| z |
| 1 |
| x |
| 1 |
| 2y |
| 1 |
| 2 |
∴
| 1 |
| z |
| 1 |
| x |
| 1 |
| 2y |
(4)3x=3log3k,4y=4log4k、6z=6log6k,又x、y、z∈R+,∴k>1,
∵
| 1 |
| 3x |
| 1 |
| 4y |
| 1 |
| 3 |
| log | 3 k |
| 1 |
| 4 |
| log | 4 k |
| log |
k |
同理可求,
| 1 |
| 4y |
| 1 |
| 6z |
| log |
k |
点评:本题考查指数式与对数式得转化,对数运算性质的应用,体现转化的数学思想,属于基础题.

练习册系列答案
相关题目
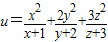 的最小值.
的最小值.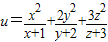 的最小值.
的最小值.