题目内容
已知直三棱柱ABC—A1B
(1)当M在C
(2)在(1)的条件下求点B到平面AMB1的距离.
解析:(1)取A

![]() B1N1⊥面A
B1N1⊥面A
则∠B1MN1为B
设C![]() a,
a,
sin∠B1MN1= .
.
解得x=a,则C![]() C
C
∴当M为CC1的中点时,B

(2)取BB1的中点K,连结MK,
则MK⊥面A1B1BA,
过K作KS⊥AB1,
连结MS,过K作KH⊥MS.

![]() KH⊥面AB
KH⊥面AB![]() KH的长为K到面AMB1的距离.
KH的长为K到面AMB1的距离.
由BB1=2B1K,则B到面AMB1的距离为K到面AMB1的距离的2倍.
在Rt△MKS中,MK=a,KS=![]() ,
,
KH= ,
,
∴K到面AB![]() .
.
∴B到面AMB1的距离为![]() .
.

练习册系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.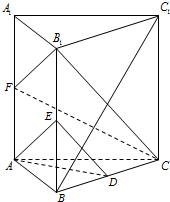 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.