题目内容
设数列{an}的前项的和Sn= (an-1) (n
(an-1) (n +),(1)求a1;a2; (2)求证数列{an}为等比数列。
+),(1)求a1;a2; (2)求证数列{an}为等比数列。
【答案】
(1)
 ,
, .(2)见解析。
.(2)见解析。
【解析】
试题分析:(Ⅰ)由 ,得
,得
∴
 又
又 ,即
,即 ,得
,得 .
.
(Ⅱ)当n>1时,
得 所以
所以 是首项
是首项 ,公比为
,公比为 的等比数列.
的等比数列.
考点:本题主要考查等比数列的概念及通项公式。
点评:已知数列的前项的和Sn求通项公式,属于数列的基本问题,要特别注意检验n=1的情况是否适合 的式子。
的式子。

练习册系列答案
相关题目
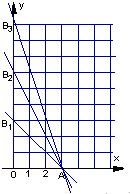 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组