��Ŀ����
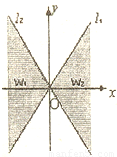
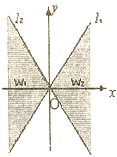 ��ͼ��ֱ��ll��y=2x��ֱ��l2��y=-2x֮�����Ӱ�������߽磩��Ϊw������벿�ּ�Ϊw1���Ұ벿�ּ�ΪW2��
��ͼ��ֱ��ll��y=2x��ֱ��l2��y=-2x֮�����Ӱ�������߽磩��Ϊw������벿�ּ�Ϊw1���Ұ벿�ּ�ΪW2����1���ֱ��ò���ʽ���ʾw1��w2��
��2��������W�еĶ���P��x��y����l1��l2�ľ���֮������4�����P�Ĺ켣C�ķ��̣�
��3���費��ԭ���ֱ��l������C�ཻ��Ml��M2���㣬����ll��l2��ֱ���M3��M4���㣮��֤��OMlM2���������OM3M4�������غϣ�
���������������깫ʽ����ABC�Ķ�������ΪA��xl��y1����B��x2��y2����C��x3��y3�������ABC����������Ϊ��
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
��������1������ͼ���֪W1��ֱ��y=2x��y=-2x��벿��֮��ĵ�ļ��ϣ�W2��y=2x��y=-2x��벿��֮��ĵ�ļ��Ͻ����ɵô𰸣�
��2�����õ㵽ֱ�ߵľ��빫ʽ�����ݶ���P��x��y����l1��l2�ľ���֮������4��������ʽ�����x��y�Ĺ�ϵʽ������P�Ĺ켣���̣�
��3���ȿ���ֱ��l��x�ᴹֱʱ��ֱ��l�ķ���Ϊx=a���������M1M2��M3M4���е����꣬�жϳ���OM1M2����OM3M4���������궼Ϊ��
��0�����ٿ�
ֱ��l1��x���ֱʱ�����ֱ��l�ķ�����P�Ĺ켣������������ȥy���б�ʽ����0����M1��M2�����꣬��ʾ��x1+x2��y1+y2����M3��M4�������ֱ��y=2x��y=mx+n��ʾ��x3��x4�����x3+x4=x1+x2���������y3+y4=y1+y2���ƶϳ���OM1M2���������OM3M4�������غϣ�
��2�����õ㵽ֱ�ߵľ��빫ʽ�����ݶ���P��x��y����l1��l2�ľ���֮������4��������ʽ�����x��y�Ĺ�ϵʽ������P�Ĺ켣���̣�
��3���ȿ���ֱ��l��x�ᴹֱʱ��ֱ��l�ķ���Ϊx=a���������M1M2��M3M4���е����꣬�жϳ���OM1M2����OM3M4���������궼Ϊ��
| 2a |
| 3 |
ֱ��l1��x���ֱʱ�����ֱ��l�ķ�����P�Ĺ켣������������ȥy���б�ʽ����0����M1��M2�����꣬��ʾ��x1+x2��y1+y2����M3��M4�������ֱ��y=2x��y=mx+n��ʾ��x3��x4�����x3+x4=x1+x2���������y3+y4=y1+y2���ƶϳ���OM1M2���������OM3M4�������غϣ�
����⣺��1����ͼ���֪W1��
��W2��
��
��2��������֪��
��
=4��|
-
|=1����P��W�ڣ�����
-
=1��
��3����ֱ��l��x�ᴹֱʱ������ֱ��l�ķ���Ϊx=a��a��O��������ֱ��l������C����x��
�Գƣ���ll1��l2����x��Գƣ�����M1M2��M3M4���е����궼Ϊ��a��0����
���ԡ�OM1M2����OM3M4���������궼Ϊ��
��0���������ǵ������غϣ�
��ֱ��l��x���ֱʱ����ֱ��l�ķ���Ϊy=mx+n��n��O����
��
���ã�4-m2��x2-2mnx-n2-20=0��
��ֱ��l������C��������ͬ���㣬��֪4-m2��0����
��=��2mn��2+4��4-m2����n2+20����0����1�֣�
��M1��M2������ֱ�Ϊ��xl��y1������x2��y2����
��xl+x2=
��y1+y2�Tm ��xl+x2��+2n
��M3��M4������ֱ�Ϊ��x3��x4������x4��y4����
��
��
����x3=
��x3=
�Ӷ�x3+x4=
=x1+x2
����y3+y4=m ��x3+x4��+2n=m ��x1+x2��+2n=y1+y2
����
=
��
=
����AOM1 M2���������OM3M4������Ҳ�غϣ�
|
|
��2��������֪��
| |2x-y | | ||
|
| |2x+y| | ||
|
| x2 |
| 5 |
| y2 |
| 20 |
| x2 |
| 5 |
| y2 |
| 20 |
��3����ֱ��l��x�ᴹֱʱ������ֱ��l�ķ���Ϊx=a��a��O��������ֱ��l������C����x��
�Գƣ���ll1��l2����x��Գƣ�����M1M2��M3M4���е����궼Ϊ��a��0����
���ԡ�OM1M2����OM3M4���������궼Ϊ��
| 2a |
| 3 |
��ֱ��l��x���ֱʱ����ֱ��l�ķ���Ϊy=mx+n��n��O����
��
|
��ֱ��l������C��������ͬ���㣬��֪4-m2��0����
��=��2mn��2+4��4-m2����n2+20����0����1�֣�
��M1��M2������ֱ�Ϊ��xl��y1������x2��y2����
��xl+x2=
| 2mn |
| 4-m2 |
��M3��M4������ֱ�Ϊ��x3��x4������x4��y4����
��
|
|
| n |
| 2-m |
| n |
| 2+m |
�Ӷ�x3+x4=
| 2mn |
| 4-m2 |
����y3+y4=m ��x3+x4��+2n=m ��x1+x2��+2n=y1+y2
����
| 0+x1+x2 |
| 3 |
| 0+x 3+x4 |
| 3 |
| 0+y1+y2 |
| 3 |
| 0+y3+y4 |
| 3 |
����AOM1 M2���������OM3M4������Ҳ�غϣ�
������������Ҫ������ֱ����Բ���ߵ��ۺ����⣮������ѧ���������������ν�ϵ�˼��������ۺ��Խ�ǿ���������ϴ�

��ϰ��ϵ�д�
�����Ŀ
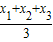 ��
��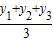 ����
����