题目内容
已知函数 ,其中常数
,其中常数 满足
满足
(1)若 ,判断函数
,判断函数 的单调性;
的单调性;
(2)若 ,求
,求 时的
时的 的取值范围.
的取值范围.
(1)Ⅰ当 ,
, 在
在 单调递增
单调递增
Ⅱ当 ,
, 在
在 单调递减
单调递减
(2) 时,
时, ;
; 时,
时,
解析试题分析: (1)由 ,说明
,说明 同号,根据指数函数在底数大于1时为增函数可得
同号,根据指数函数在底数大于1时为增函数可得 的单调性,然后由在相同区间内增函数的和为增函数,减函数的和为减函数可得函数
的单调性,然后由在相同区间内增函数的和为增函数,减函数的和为减函数可得函数 的单调性;
的单调性;
(2)由 ,说明
,说明 异号,把
异号,把 代入不等式
代入不等式 ,整理后由
,整理后由 异号,然后分类讨论求解指数不等式即可得到
异号,然后分类讨论求解指数不等式即可得到 时
时 的取值范围.
的取值范围.
试题解析:
(1)由 ,则
,则 同号
同号
Ⅰ当 ,则
,则 在
在 单调递增
单调递增
所以, 在
在 单调递增 2分
单调递增 2分
Ⅱ当 ,则
,则 在
在 单调递减
单调递减
所以, 在
在 单调递减 4分
单调递减 4分
(2)不等式 即是:
即是:
 即
即 8分
8分
因为 ,则
,则 异号
异号
Ⅰ当 ,则有
,则有 10分
10分
Ⅱ当 ,则有
,则有 12分
12分
综上, 时,
时, 
 时,
时, 14分
14分
考点:函数单调性得判断,指数不等式得求解方法,分类讨论应用.

练习册系列答案
相关题目
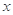 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%. ,
,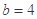 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y= 作为生态环境改造投资方案.
作为生态环境改造投资方案.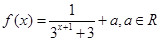
 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;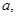 使函数
使函数 .
. 的定义域为A,求集合A;
的定义域为A,求集合A; )上单调性,并用单调性的定义加以证明.
)上单调性,并用单调性的定义加以证明.
 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数 的值;(2)求函数
的值;(2)求函数 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
 的值;(3分)
的值;(3分) 的奇偶性;(3分)
的奇偶性;(3分) ,求
,求 的取值范围.(6分)
的取值范围.(6分) 为奇函数,且当
为奇函数,且当 时,
时, .当
.当 时,
时, ,最小值为
,最小值为 ,求
,求 的值.
的值. 的函数
的函数 是奇函数.
是奇函数.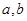 的值;
的值; 的单调性,并证明.
的单调性,并证明.