题目内容
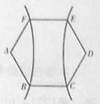 如图,正六边形ABCDEF的两个顶点,A、D为双曲线的两个焦点,其余4个顶点都在双曲线上,则该双曲线的离心率是( )
如图,正六边形ABCDEF的两个顶点,A、D为双曲线的两个焦点,其余4个顶点都在双曲线上,则该双曲线的离心率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:利用余弦定理求得 AE,由双曲线的定义可得2a=AE-DE 的值,由此求出 e=
的值.
| c |
| a |
解答:解:设正六边形ABCDEF的边长为1,中心为 O,以AD所在直线为x轴,以 O 为原点,建立直角坐标系,
则 c=1,△AEF中,由余弦定理得AE2=AF2+EF2-2AF•EFcos120°=1+1-2(-
)=3,
∴AE=
,2a=AE-DE=
-1,a=
,∴e=
=
=
+1,
故选 A.
则 c=1,△AEF中,由余弦定理得AE2=AF2+EF2-2AF•EFcos120°=1+1-2(-
| 1 |
| 2 |
∴AE=
| 3 |
| 3 |
| ||
| 2 |
| c |
| a |
| 1 | ||||
|
| 3 |
故选 A.
点评:本题考查双曲线的定义和双曲线的标准方程,以及双曲线的简单性质的应用,计算2a=AE-DE 的值是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目

 如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,
如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1, 16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:
16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中: 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为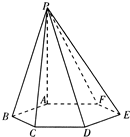 (2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )
(2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )