题目内容
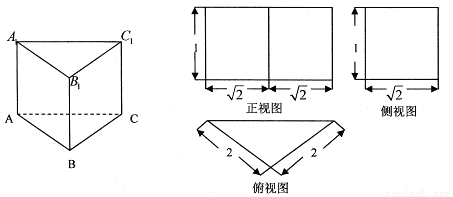
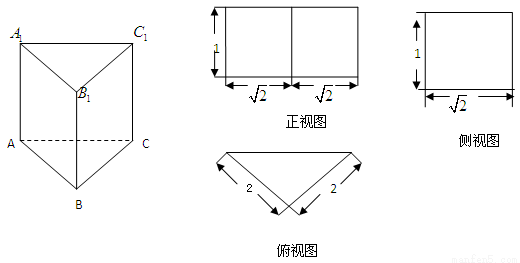
已知直三棱柱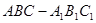 的三视图如图所示,
的三视图如图所示, 是
是 的中点.
的中点.
(Ⅰ)求证: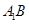 ∥平面
∥平面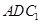 ;
;
(Ⅱ)求二面角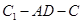 的余弦值;
的余弦值;
(Ⅲ)试问线段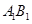 上是否存在点
上是否存在点 ,使
,使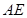 与
与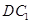 成
成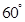 角?若存在,确定
角?若存在,确定 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.
【答案】
(Ⅰ)根据三视图知:三棱柱 是直三棱柱,
是直三棱柱, ,
, 连结
连结 ,交
,交 于点
于点 ,连结
,连结 .由
.由
 是直三棱柱,得四边形
是直三棱柱,得四边形 为矩形,
为矩形, 为
为 的中点,又
的中点,又 为
为 中点,所以
中点,所以 为
为 中位线,所以
中位线,所以  ∥
∥ 所以
所以  ∥平面
∥平面
(Ⅱ) (Ⅲ)
(Ⅲ) 为线段
为线段 中点
中点
【解析】
试题分析:(Ⅰ)证明:根据三视图知:三棱柱 是直三棱柱,
是直三棱柱, ,
, 连结
连结 ,交
,交 于点
于点 ,连结
,连结 .由
.由
 是直三棱柱,
是直三棱柱,
得四边形 为矩形,
为矩形, 为
为 的中点.
的中点.
又 为
为 中点,所以
中点,所以 为
为 中位线,所以
中位线,所以  ∥
∥ ,
2分
,
2分
因为  平面
平面 ,
, 平面
平面 ,
,
所以  ∥平面
∥平面 .
4分
.
4分
(Ⅱ)解:由 是直三棱柱,且
是直三棱柱,且 ,故
,故 两两垂直.
两两垂直.
如图建立空间直角坐标系 .
5分
.
5分


 ,则
,则 .
.
所以  ,
,
设平面 的法向量为
的法向量为 ,则有
,则有

所以  取
取 ,得
,得 .
6分
.
6分
易知平面 的法向量为
的法向量为 .
.
由二面角 是锐角,得
是锐角,得  .
.
所以二面角 的余弦值为
的余弦值为 .
8分
.
8分
(Ⅲ)解:假设存在满足条件的点 .
.
因为 在线段
在线段 上,
上, ,
, ,故可设
,故可设 ,其中
,其中 .
.
所以  ,
, .
9分
.
9分
因为 与
与 成
成 角
10分
角
10分
所以 ,解得
,解得 ,舍去
,舍去 .
.
所以当点 为线段
为线段 中点时,
中点时, 与
与 成
成 角.
12分
角.
12分
考点:空间线面平行的判定及二面角线线角的求解
点评:采用空间向量法求解立体几何问题首先要找到直线的方向向量和平面的法向量,直线的方向向量和平面的法向量垂直时,直线与平面平行;求二面角可先求出法向量的夹角,求两条异面直线所成角可首先求两直线的方向向量所成角

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009•普陀区一模)如图,在空间直角坐标系中,已知直三棱柱的顶点A在x轴上,AB平行于y轴,侧棱AA1平行于z轴.当顶点C在y轴正半轴上运动时,以下关于此直三棱柱三视图的表述正确的是( )
(2009•普陀区一模)如图,在空间直角坐标系中,已知直三棱柱的顶点A在x轴上,AB平行于y轴,侧棱AA1平行于z轴.当顶点C在y轴正半轴上运动时,以下关于此直三棱柱三视图的表述正确的是( )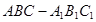 的三视图如图所示,且
的三视图如图所示,且 是
是 的中点.
的中点.
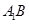 ∥平面
∥平面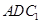 ;
;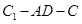 的余弦值;
的余弦值;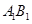 上是否存在点
上是否存在点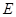 ,使
,使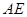 与
与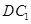 成
成 角?若存在,确定
角?若存在,确定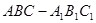 的三视图如图所示,且
的三视图如图所示,且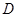 是
是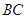 的中点.
的中点.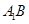 ∥平面
∥平面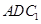 ;
;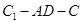 的余弦值;
的余弦值;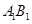 上是否存在点
上是否存在点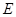 ,使
,使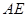 与
与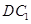 成
成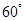 角?若存在,确定
角?若存在,确定