题目内容
在△ABC中,2
(sin2A-sin2C)=(a-b)sinB,它的外接圆半径为
.(1)求角C的大小.
(2)求
·
的最大值.
解:(1)由正弦定理得sinA=,sinB=,sinC=.
2［(
)2-(
)2］=(a-b)
,a2-c2=ab-b2,∴
=
.
∴cosC=
,C=
.
(2)
·
=b·a·cosC=
ab=
·(2
sinA)(2
sinB)=4sinA·sin(
-A)=4sinA·(
cosA+
sinA)=2(
sinAcosA+sin2A)=2(
sin2A+
)=2sin(2A-
)+1.
∵A∈(0,
),∴2A-
∈(-
,
).∴2A-
=
,即A=
时,(
·
)max=3.
练习册系列答案
相关题目
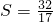时，求ab的值．
时，求ab的值．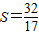
时，求ab的值．