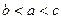题目内容
若函数 的图象与
的图象与 轴所围成的封闭图形的面积为
轴所围成的封闭图形的面积为 ,则
,则 的展开式中常数项为
的展开式中常数项为
 的图象与
的图象与 轴所围成的封闭图形的面积为
轴所围成的封闭图形的面积为 ,则
,则 的展开式中常数项为
的展开式中常数项为 A. | B. | C. | D.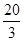 |
D
本题考查定积分的计算以及二项式定理.
设函数 与
与 轴围成的封闭图形的面积为
轴围成的封闭图形的面积为 ,
,
则有
下面分别计算 和
和
因为 ,所以
,所以 的原函数为
的原函数为 ,
,
所以
又 ,则
,则 的原函数为
的原函数为 ,所以
,所以
所以所求的面积
设二项展开式 中的第
中的第 项为
项为
若第 项为常数项,则
项为常数项,则 ,即
,即 ,解得
,解得 ,此时有
,此时有
因为 ,所以
,所以
故正确答案为D
设函数
 与
与 轴围成的封闭图形的面积为
轴围成的封闭图形的面积为 ,
,则有

下面分别计算
 和
和
因为
 ,所以
,所以 的原函数为
的原函数为 ,
,所以

又
 ,则
,则 的原函数为
的原函数为 ,所以
,所以
所以所求的面积

设二项展开式
 中的第
中的第 项为
项为
若第
 项为常数项,则
项为常数项,则 ,即
,即 ,解得
,解得 ,此时有
,此时有
因为
 ,所以
,所以
故正确答案为D
 |

练习册系列答案
相关题目
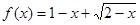 的值域为( )
的值域为( )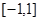
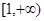

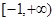
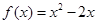 ,
,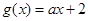 (
(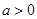 ),若
),若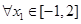 ,
,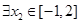 ,使得
,使得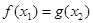 ,则实数
,则实数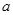 的取值范围是
的取值范围是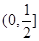
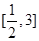
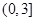
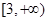




 的定义域为集合
的定义域为集合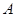 ,函数
,函数 的定义域为集合
的定义域为集合 ,则
,则




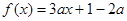 ,在区间
,在区间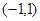 上存在一个零点,则
上存在一个零点,则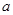 的取值范围是
的取值范围是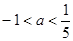
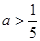
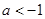

 ,
, ,
,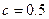 ,则它们的大小关系是
,则它们的大小关系是