题目内容
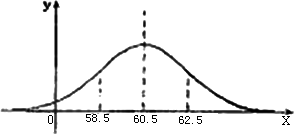
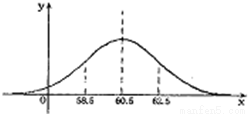
 某单位1000名青年职员在体重x(kg)服从正态分布N(μ,22),且正态分布的密度曲线如图所示,若58.5~62.5kg体重属于正常情况,则这1000名青年职员中体重属于正常情况的人数约是(其中Φ(1)≈0.841)
某单位1000名青年职员在体重x(kg)服从正态分布N(μ,22),且正态分布的密度曲线如图所示,若58.5~62.5kg体重属于正常情况,则这1000名青年职员中体重属于正常情况的人数约是(其中Φ(1)≈0.841)
- A.682
- B.841
- C.341
- D.667
A
分析:设出变量,根据x~N(μ,22)得到y~N(0,1),根据58.5~62.5kg体重属于正常情况,求p(x<62.5)-p(x<58.5)的结果,根据两个变量之间的关系和条件中所给的φ(1)=0.841,得到结果.
解答:令
∵x~N(μ,22)
∴y~N(0,1)
∴p(x<62.5)-p(x<58.5)=p(y<1)-p(y<-1)
=φ(1)-φ(-1)=φ(1)-[1-φ(1)]=2φ(1)-1=2×0.841-1=0.682
∴体重属于正常情况的人数约是0.682×1000≈682.
故选A.
点评:本题考查正态曲线的特点及曲线所表示的意义,考查求在一定范围中的数据所占的概率,考查数形结合思想.属于基础题.
分析:设出变量,根据x~N(μ,22)得到y~N(0,1),根据58.5~62.5kg体重属于正常情况,求p(x<62.5)-p(x<58.5)的结果,根据两个变量之间的关系和条件中所给的φ(1)=0.841,得到结果.
解答:令

∵x~N(μ,22)
∴y~N(0,1)
∴p(x<62.5)-p(x<58.5)=p(y<1)-p(y<-1)
=φ(1)-φ(-1)=φ(1)-[1-φ(1)]=2φ(1)-1=2×0.841-1=0.682
∴体重属于正常情况的人数约是0.682×1000≈682.
故选A.
点评:本题考查正态曲线的特点及曲线所表示的意义,考查求在一定范围中的数据所占的概率,考查数形结合思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某单位1000名青年职员在体重x(kg)服从正态分布N(μ,22),且正态分布的密度曲线如图所示,若58.5~62.5kg体重属于正常情况,则这1000名青年职员中体重属于正常情况的人数约是(其中Φ(1)≈0.841)( )
某单位1000名青年职员在体重x(kg)服从正态分布N(μ,22),且正态分布的密度曲线如图所示,若58.5~62.5kg体重属于正常情况,则这1000名青年职员中体重属于正常情况的人数约是(其中Φ(1)≈0.841)( )