题目内容
已知四棱锥
的底面
是直角梯形，
平面,
若平面
与平面
所成二面角的余弦值为
，求
的值。
解析：以点
为坐标原点, 以
分别为
轴,建立如图空间直角坐标系,
不妨设 
则
所以
设平面
的法向量为
则
①
②
不妨设
则
即
………………2分
又因为 
平面
所以 
又因为 
∥
所以 
故
平面
即
是平面
的一个法向量,
且
…………………………………………4分
因为
= 
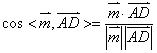……………………………………………………6分
又平面
与平面所成二面角的余弦值为
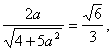解得
因此
． ……………10分 
练习册系列答案
相关题目
已知直四棱柱ABCD-A1B1C1D1的底面是菱形AC∩BD=0，AB=2，∠ABC=60°，E、F分别为棱CC1，BB1上的点，EC=BC=2FB，M是AE的中点．