Question

如图，在Rt△ABC中，已知BC=a，若长为2a的线段PQ以点A为中点，问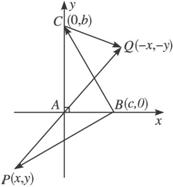与的夹角θ取何值时，·的值最大？并求出这个最大值.

Answer 1

思路分析：解答本题的关键是要结合图形，利用向量的三角形法则找出向量之间的关系；或建立适当的坐标系，利用向量的坐标形式来解答.

解法1：∵⊥,∴·=0,∵=-,=-,=-, ∴·=(-)·(-)=·-·-·+·=-a²-·+·=-a²+·(-)=-a²+12·=-a²+a²cosθ.故

当cosθ=1,即θ=0(与方向相同)时，·最大，其最大值为0.

解法2：以直角顶点A为坐标原点，两直角边所在直线为坐标轴，建立如右图所示的平面直角坐标系.设|AB|=c，|AC|=b，则A（0，0），B（c,0）,

C(0,b),且|PQ|=2a，|BC|=a.设点P的坐标为（x,y），则Q（-x,-y）.

∴=(x-c,y), =(-x,-y-b),

=(-c,b), =(-2x,-2y).∴·=(x-c)(-x)+y(-y-b)=-(x²+y²)+cx-by.

∵cosθ=,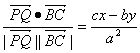

∴cx-by=a²cosθ,∴·=-a²+a²cosθ,故当cosθ=1,即θ=0(与方向相同)时，·最大，其最大值为0.

答案：θ=0时，·最大为0.