题目内容
定义在 上的函数
上的函数 满足
满足 .当
.当 时,
时,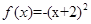 ,当
,当 时,
时, 。则
。则 ( )
( )
| A.335 | B.338 | C.1678 | D.2012 |
B
解析试题分析:解:因为在 上的函数
上的函数 满足
满足 ,周期为6,当
,周期为6,当 时,
时,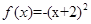 ,当,
,当, 时,
时, ,因此可知f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值,故
,因此可知f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值,故 ,选B
,选B
考点:函数的周期性
点评:利用已知的关系式赋值法来求解周期,进而化简求值,属于基础题。

练习册系列答案
相关题目
设函数 的图象上的点
的图象上的点 处的切线的斜率为
处的切线的斜率为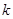 ,记
,记 ,则函数
,则函数 的图象大致为( )
的图象大致为( )
| A. | B. | C. | D. |
已知函数 在
在 上两个零点,则
上两个零点,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
已知f(x)是定义在(0,+ )上的非负可导函数,且满足
)上的非负可导函数,且满足 。对任意正数a、b,若a<b,则必有( )
。对任意正数a、b,若a<b,则必有( )
| A.af(b)≤bf(a) | B.bf(a)≤af(b) |
| C.af(a)≤f(b) | D. bf(b)≤f(a) |
设函数f (x)是(- ,+
,+ )上的减函数,又若a
)上的减函数,又若a R,则( )
R,则( )
| A.f (a)>f (2a) | B.f (a2)<f (a) |
| C.f (a2+a)<f (a) | D.f (a2+1) <f (a) |
函数 的单调递减区间是( )
的单调递减区间是( )
A. ,+∞) ,+∞) | B.(-∞, | C.(0, | D.[e,+∞) |
下列函数中,既是奇函数又是增函数的为( )
A. | B. | C. | D. |
已知函数 的定义域为R,当
的定义域为R,当 时,
时,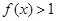 ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列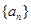 满足
满足 ,且
,且
( N*),则
N*),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
 的部分图象,其中
的部分图象,其中 ,则下列所给图象中可能正确的是 ( )
,则下列所给图象中可能正确的是 ( )