题目内容
已知正四棱锥S－ABCD中，SA＝3，那么当该棱锥的体积最大时，它的高为______．
设底面边长为a，则高h＝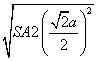
＝
，所以体积
V＝
a2h＝
，设y＝9a4－
a6，则y′＝36a3－3a5，
当y取最值时，y′＝36a3－3a5＝0，解得a＝0或a＝2
，
故当a＝2时，体积最大，此时高h＝.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
已知正四棱锥S－ABCD中，SA＝3，那么当该棱锥的体积最大时，它的高为______．
设底面边长为a，则高h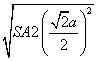＝＝，所以体积
V＝a2h＝，设y＝9a4－a6，则y′＝36a3－3a5，
当y取最值时，y′＝36a3－3a5＝0，解得a＝0或a＝2，
故当a＝2时，体积最大，此时高h＝.
阅读快车系列答案
（文做理不做）已知：正四棱锥S-ABCD的高为