题目内容
设数列{an}的前n项和为sn，a1=1，an=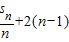
，（n∈N*），若s1+
+
+…+
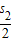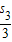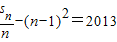，则n的值为（ ）A．1007
B．1006
C．2012
D．2013
【答案】分析：由已知利用sn-sn-1=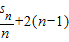
，（n≥2），整理可得
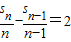，结合等差数列的求和公式可求s1+
+
+…+
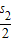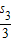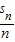，然后代入已知条件中即可求解n
解答：解：∵an=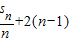
，
∴sn-sn-1=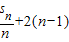
，（n≥2）
整理可得，（n-1）sn-nsn-1=2n（n-1）
两边同时除以n（n-1）可得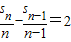
∴数列{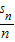
}是以
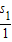=1为首项，以2为公差的等差数列
∴s1+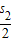
+
+…+
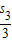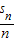-（n-1）2
=
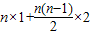-（n-1）2
=n2-（n-1）2
=2n-1
由题意可得，2n-1=2013
解可得n=1007
故选A
点评：本题主要考查了利用数列的递推公式构造等差数列求解通项公式，解题的关键是对已知灵活变形
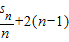，（n≥2），整理可得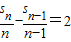，结合等差数列的求和公式可求s1+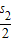++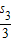…+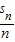，然后代入已知条件中即可求解n解答：解：∵an=
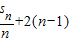，∴sn-sn-1=
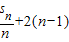，（n≥2）整理可得，（n-1）sn-nsn-1=2n（n-1）
两边同时除以n（n-1）可得
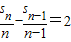
∴数列{
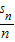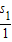}是以=1为首项，以2为公差的等差数列∴s1+
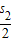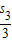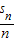++…+-（n-1）2=
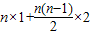-（n-1）2=n2-（n-1）2
=2n-1
由题意可得，2n-1=2013
解可得n=1007
故选A
点评：本题主要考查了利用数列的递推公式构造等差数列求解通项公式，解题的关键是对已知灵活变形
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目