题目内容
正三棱锥的底面边长为2,侧面均为直角三角形,则此棱锥的体积为( )
A.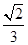 | B.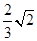 | C.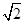 | D.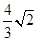 |
A
专题:计算题.
分析:先求正三棱锥的侧棱长,然后求出体积.
解答:解:由题意正三棱锥的底面边长为2,侧面均为直角三角形,
可知:侧棱长为
 ,三条侧棱两两垂直,
,三条侧棱两两垂直,所以此三棱锥的体积为
 ×
× ×
× ×
× ×
× =
=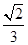
故选A.
点评:本题考查棱锥的体积,考查学生的空间想象能力,逻辑思维能力,是基础题.

练习册系列答案
相关题目
题目内容
A.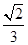 | B.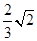 | C.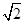 | D.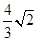 |
 ,三条侧棱两两垂直,
,三条侧棱两两垂直, ×
× ×
× ×
× ×
× =
=