题目内容

如果函数y=x²-2tx与y=2sin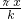 $数学公式$ （x＞0，k＞0）在某一点取得相等的最小值，则k的最大值是________．

$\text{[math]}$
分析：先根据二次函数的性质，知数y=x²-2tx在x=t时取得最小值-t²，再根据正弦函数的性质，知函数y=2sin 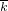$\text{[math]}$ （x＞0，k＞0）在x=2mk- $\text{[math]}$ （m∈Z）时取得最小值-2，由已知得两函数在同一点取得同样的最值，故可得-t²=-2，2mk- $\text{[math]}$ =t （m∈Z），从而将k用整数变量m表示，求最值即可
解答：函数y=x²-2tx在x=t时取得最小值-t²，
函数y=2sin 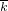$\text{[math]}$ （x＞0，k＞0）在x=2mk- $\text{[math]}$ （m∈Z）时取得最小值-2
∵函数y=x²-2tx与y=2sin 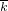$\text{[math]}$ （x＞0，k＞0）在某一点取得相等的最小值
∴-t²=-2，∵t＞0
∴t= $\text{[math]}$
∴2mk- $\text{[math]}$ = $\text{[math]}$ （m∈Z）
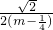∴k= $\text{[math]}$ （m∈Z）
∴m=1时，k取得最大值 $\text{[math]}$ = $\text{[math]}$
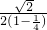故答案为 $\text{[math]}$
点评：本题考查了二次函数的图象和性质，正弦函数的图象和性质，转化化归的思想方法