题目内容
已知 ≤x≤
≤x≤ ,则
,则
(1)1-x的取值范围是[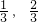 ];
];
(2)x(1-x)的取值范围是[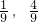 ].
].
以上命题是否正确,若错误予以纠正;若正确,请予以证明.
解:(1)该命题正确.
∵ ≤x≤
≤x≤ ,∴-
,∴- ≤-x≤-
≤-x≤- .∴
.∴ ≤1-x≤
≤1-x≤ ,
,
即1-x的取值范围是[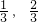 ].
].
(2)该命题是假命题.
∵x(1-x)=-x2+x=-(x- )2+
)2+ 在[
在[ ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减.
]上单调递减.
∴当x= 时,取到最大值是
时,取到最大值是 ;当x=
;当x= 或
或 时,取到最小值
时,取到最小值 ,
,
故x(1-x)的取值范围是[ ]
]
分析:(1)由x的范围求出-x的范围,再求出1-x的范围,注意不等式两边同乘负数,不等号要发生改变;
(2)利用配方法将x(1-x)进行变形,判断出在区间[ ,
, ]上的单调性,从而求出最值,即求出x(1-x)的取值范围.
]上的单调性,从而求出最值,即求出x(1-x)的取值范围.
点评:本题的考点是在给定区间上求函数的最值,对于简单的函数利用不等式求解,注意同乘一个负数时不等号方向改变,对于二次函数用配方法变形后,判断出在区间上的单调性,再求最值和值域.
∵
 ≤x≤
≤x≤ ,∴-
,∴- ≤-x≤-
≤-x≤- .∴
.∴ ≤1-x≤
≤1-x≤ ,
,即1-x的取值范围是[
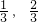 ].
].(2)该命题是假命题.
∵x(1-x)=-x2+x=-(x-
 )2+
)2+ 在[
在[ ]上单调递增,在[
]上单调递增,在[ ,
, ]上单调递减.
]上单调递减.∴当x=
 时,取到最大值是
时,取到最大值是 ;当x=
;当x= 或
或 时,取到最小值
时,取到最小值 ,
,故x(1-x)的取值范围是[
 ]
]分析:(1)由x的范围求出-x的范围,再求出1-x的范围,注意不等式两边同乘负数,不等号要发生改变;
(2)利用配方法将x(1-x)进行变形,判断出在区间[
 ,
, ]上的单调性,从而求出最值,即求出x(1-x)的取值范围.
]上的单调性,从而求出最值,即求出x(1-x)的取值范围.点评:本题的考点是在给定区间上求函数的最值,对于简单的函数利用不等式求解,注意同乘一个负数时不等号方向改变,对于二次函数用配方法变形后,判断出在区间上的单调性,再求最值和值域.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 ≤x≤
≤x≤ ,则
,则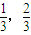 ];
];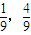 ].
].