题目内容
设F1,F2是椭圆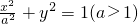 的两个焦点,点P是该椭圆上的动点,若∠F1PF2的最大值为
的两个焦点,点P是该椭圆上的动点,若∠F1PF2的最大值为 .
.
(1)求该椭圆的方程;
(2)求以该椭圆的长轴AB为一底,另一底CD的两端点也在椭圆上的梯形ABCD的最大面积.
解:(1)由于∠F1PF2的最大值为 ,则P 的坐标为(0,±1),即c=1
,则P 的坐标为(0,±1),即c=1
∵b=1,∴
∴椭圆的方程为:
(2)由于AB∥CD,所以C,D关于y轴对称,设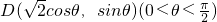
则梯形的面积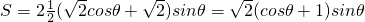 ,
,
记f(θ)=(cosθ+1)sinθ,则f'(θ)=cos2θ-sin2θ+cosθ=2cos2θ+cosθ-1=0得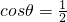 ,即
,即
当 时,f'(θ)>0,f(θ)在
时,f'(θ)>0,f(θ)在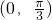 单调递增;
单调递增;
当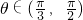 时,f'(θ)<0,f(θ)在
时,f'(θ)<0,f(θ)在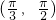 单调递增;
单调递增;
所以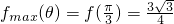 ,故
,故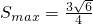
分析:(1)根据∠F1PF2的最大值为 ,可得c=1,又b=1,所以
,可得c=1,又b=1,所以 ,从而可得椭圆的方程;
,从而可得椭圆的方程;
(2)设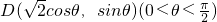 ,则梯形的面积
,则梯形的面积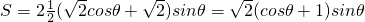 ,构建函数f(θ)=(cosθ+1)sinθ,确定函数的单调性,从而可得函数的最值,即可求得梯形ABCD的最大面积.
,构建函数f(θ)=(cosθ+1)sinθ,确定函数的单调性,从而可得函数的最值,即可求得梯形ABCD的最大面积.
点评:本题考查椭圆的标准方程,考查求函数的最值,解题的关键是正确设点,利用三角函数解决问题.
 ,则P 的坐标为(0,±1),即c=1
,则P 的坐标为(0,±1),即c=1∵b=1,∴

∴椭圆的方程为:

(2)由于AB∥CD,所以C,D关于y轴对称,设
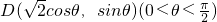
则梯形的面积
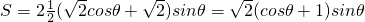 ,
,记f(θ)=(cosθ+1)sinθ,则f'(θ)=cos2θ-sin2θ+cosθ=2cos2θ+cosθ-1=0得
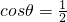 ,即
,即
当
 时,f'(θ)>0,f(θ)在
时,f'(θ)>0,f(θ)在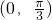 单调递增;
单调递增;当
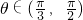 时,f'(θ)<0,f(θ)在
时,f'(θ)<0,f(θ)在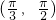 单调递增;
单调递增;所以
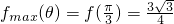 ,故
,故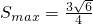
分析:(1)根据∠F1PF2的最大值为
 ,可得c=1,又b=1,所以
,可得c=1,又b=1,所以 ,从而可得椭圆的方程;
,从而可得椭圆的方程;(2)设
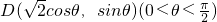 ,则梯形的面积
,则梯形的面积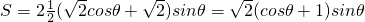 ,构建函数f(θ)=(cosθ+1)sinθ,确定函数的单调性,从而可得函数的最值,即可求得梯形ABCD的最大面积.
,构建函数f(θ)=(cosθ+1)sinθ,确定函数的单调性,从而可得函数的最值,即可求得梯形ABCD的最大面积.点评:本题考查椭圆的标准方程,考查求函数的最值,解题的关键是正确设点,利用三角函数解决问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
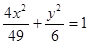 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且 ,
, 的面积为( )
的面积为( ) D.
D.