题目内容
设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记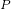 ={n∈N|f(n)∈P},
={n∈N|f(n)∈P}, ={n∈N|f(n)∈Q},则(
={n∈N|f(n)∈Q},则(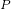 ∩CN
∩CN )∪(
)∪( ∩
∩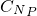 )=
)=
- A.{0,3}
- B.{1,2}
- C.(3,4,5}
- D.{1,2,6,7}
A
分析:先根据新的定义求出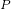 和
和 ,然后根据补集和交集的定义求出
,然后根据补集和交集的定义求出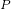 ∩CN
∩CN 和
和 ∩
∩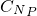 ,最后根据并集的定义求出(
,最后根据并集的定义求出(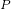 ∩CN
∩CN )∪(
)∪( ∩
∩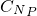 )即可.
)即可.
解答: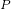 ={n∈N|f(n)∈P}={0,1,2};
={n∈N|f(n)∈P}={0,1,2};
 ={n∈N|f(n)∈Q}={1,2,3};
={n∈N|f(n)∈Q}={1,2,3};
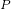 ∩CN
∩CN ={0},
={0}, ∩
∩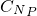 ={3}
={3}
∴(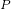 ∩CN
∩CN )∪(
)∪( ∩
∩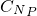 )={0,3}
)={0,3}
故选A
点评:本题主要考查了交、并、补集的混合运算,以及新定义,属于创新题,考查了阅读题意的能力.
分析:先根据新的定义求出
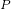 和
和 ,然后根据补集和交集的定义求出
,然后根据补集和交集的定义求出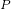 ∩CN
∩CN 和
和 ∩
∩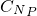 ,最后根据并集的定义求出(
,最后根据并集的定义求出(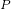 ∩CN
∩CN )∪(
)∪( ∩
∩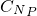 )即可.
)即可.解答:
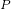 ={n∈N|f(n)∈P}={0,1,2};
={n∈N|f(n)∈P}={0,1,2}; ={n∈N|f(n)∈Q}={1,2,3};
={n∈N|f(n)∈Q}={1,2,3};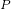 ∩CN
∩CN ={0},
={0}, ∩
∩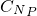 ={3}
={3}∴(
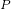 ∩CN
∩CN )∪(
)∪( ∩
∩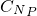 )={0,3}
)={0,3}故选A
点评:本题主要考查了交、并、补集的混合运算,以及新定义,属于创新题,考查了阅读题意的能力.

练习册系列答案
相关题目
设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q={3,4,5,6,7},记
={n∈N|f(n)∈P},
={n∈N|f(n)∈Q},则(
∩CN
)∪(
∩CN
)=( )
| ? |
| P |
| ? |
| Q |
| ? |
| P |
| ? |
| Q |
| ? |
| Q |
| ? |
| P |
| A、{0,3} |
| B、{1,2} |
| C、{3,4,5} |
| D、{1,2,6,7} |
 ={n∈N|f(n)∈P},
={n∈N|f(n)∈P}, ={n∈N|f(n)∈Q},则(
={n∈N|f(n)∈Q},则(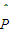 ∩CN
∩CN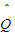 )∪(
)∪(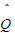 ∩
∩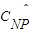 )=( )
)=( )