Question

在三棱锥P—ABC中,PC⊥平面ABC,∠ACB=90°,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.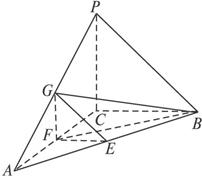

(1)求证:平面GFE∥平面PCB;

(2)求GB与平面ABC所成角的正切值;

(3)求二面角A-PB-C的大小.

Answer 1

解法一:(1)证明:因为E、F、G分别是AB、AC、PA的中点,

则EF∥BC,GF∥PC,

且EF、GF平面PCB,

所以EF∥平面PCB,GF∥平面PCB.

又EF∩GF=F,

所以平面GFE∥平面PCB.

(2)连结BF,因为GF∥PC,PC⊥平面ABC,

所以GF⊥平面ABC,BF为斜线BG在平面ABC上的射影,则∠GBF为所求.

GF=PC=,在Rt△BCF中,可求得BF=.

在Rt△GBF中,tan∠GBF==,

即BG与平面ABC所成角的正切值是.

(3)设PB的中点为H,连结HC,AH,

因为△PBC为等腰直角三角形,

所以HC⊥PB.

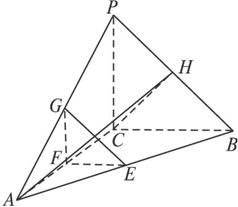
又AC⊥BC,AC⊥PC,且BC∩PC=C,

所以AC⊥平面PCB.

由三垂线定理得AH⊥PB.

所以∠AHC为二面角APBC的平面角.

因为AC=2,HC=,所以tan∠AHC==2.

所以∠AHC=arctan2,

即二面角APBC的大小是arctan2.

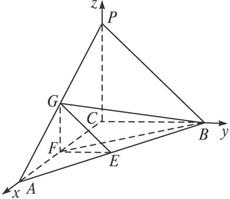
解法二:依条件建立如图所示空间直角坐标系.

所以A(2,0,0),B(0,1,0),P(0,0,1).

(1)略.

(2)连结BF,因为GF∥PC,PC⊥平面ABC,

所以GF⊥平面ABC,BF为斜线BG在平面ABC上的射影,则∠GBF为所求.

因为F、G分别为AC、AP的中点,F(1,0,0),G(1,0,),=(1,-1,0),

=(1,-1,),||=,||=,cos∠GB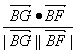F==.tan∠GBF=.

(3)显然=(2,0,0)是平面PBC的一个法向量.设n=(x,y,z)是平面PAB的一个法向量,

因为=(-2,0,1),=(-2,1,0),所以由n·=0,n·=0,解得n=(1,2,2).

设二面角A-PB-C的大小为θ,由图可知,与n的大小也为θ.所以cosθ==.

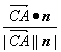所以二面角A-PB-C的大小为arccos(arccos=arctan2).