题目内容
（本小题满分12分）
某市文化馆在春节期间举行高中生“蓝天海洋杯”象棋比赛，规则如下：两名选手比赛时，每局胜者得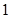
分，负者得
分，比赛进行到有一人比对方多
分或打满
局时结束.假设选手甲与选手乙比赛时，甲每局获胜的概率皆为
，且各局比赛胜负互不影响.
（Ⅰ）求比赛进行
局结束，且乙比甲多得分的概率；
（Ⅱ）设
表示比赛停止时已比赛的局数，求随机变量的分布列和数学期望．
（Ⅰ）
.（Ⅱ）由随机变量的分布列为
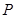
解析试题分析：（Ⅰ）由题意知，乙每局获胜的概率皆为
.…………1分
比赛进行局结束，且乙比甲多得分即头两局乙胜一局，3,4局连胜，则
. …………4分
（Ⅱ）由题意知，的取值为
. ………5分
则
…………6分
…………7分
…………9分
所以随机变量的分布列为
………10分
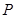
则…………12
考点：本题考查了随机事件的概率、分布列及期望的求法
点评：，考查了学生的计算能力及解决实际问题的能力，掌握求分布列的步骤及期望公式是解决此类问题的关键
练习册系列答案
相关题目
次，求在这一枪出现空弹的概率；
次，求在这三枪中出现空弹的概率
四个不同的岗位服务，每个岗位至少有一名志愿者．（Ⅰ）求甲、乙两人同时参加
岗位服务的概率；（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；（Ⅲ）设随机变量
为这五名志愿者中参加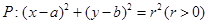
被y轴所截的弦长为2，被x轴分成两段弧，且弧长之比等于
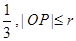（其中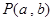
为圆心，O为坐标原点）。
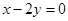上的投影为A，求事件“在圆P内随机地投入一点，使这一点恰好在
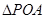内”的概率的最大值
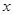的分布列和数学期望。