题目内容
已知函数f(x)= 是奇函数(a为常数).
是奇函数(a为常数).
(1)求a的值;
(2)解不等式f(x)< .
.
解:(1)由题意,f(0)=0,即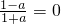 ,解得a=1;
,解得a=1;
(2)f(x)< ,即
,即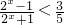 ,∵2x+1>0,∴2x<4,∴x<2,∴不等式的解集为(-∞,2).
,∵2x+1>0,∴2x<4,∴x<2,∴不等式的解集为(-∞,2).
分析:(1)根据函数在全体实数上有定义,函数又是一个奇函数,得到函数在自变量0的取值是0,写出关于a的方程,解方程即可.
(2)f(x)< ,即
,即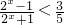 ,可以求得.
,可以求得.
点评:本题考查函数的奇偶性,利用函数在自变量0的取值是0,简化解题.
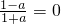 ,解得a=1;
,解得a=1;(2)f(x)<
 ,即
,即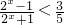 ,∵2x+1>0,∴2x<4,∴x<2,∴不等式的解集为(-∞,2).
,∵2x+1>0,∴2x<4,∴x<2,∴不等式的解集为(-∞,2).分析:(1)根据函数在全体实数上有定义,函数又是一个奇函数,得到函数在自变量0的取值是0,写出关于a的方程,解方程即可.
(2)f(x)<
 ,即
,即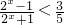 ,可以求得.
,可以求得.点评:本题考查函数的奇偶性,利用函数在自变量0的取值是0,简化解题.

练习册系列答案
相关题目
已知函数f(x+1)是偶函数,当x2>x1>1时,[f(x2)-f(x1)]( x2-x1)>0恒成立,设a=f (-
),b=f(2),c=f(3),则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |