题目内容
已知⊙O方程为![]() ,圆外有一定点
,圆外有一定点![]() ,求过点A且和⊙O相切的动圆圆心的轨迹。
,求过点A且和⊙O相切的动圆圆心的轨迹。
解法一:设动圆圆心为P![]() ,定圆圆心为(0,1),半径为1,由题可知动圆半径为
,定圆圆心为(0,1),半径为1,由题可知动圆半径为![]() 。
。
⊙P与定⊙O作外切时,有![]()
⊙P与⊙O内切时有![]()
综上有![]()
即 ![]()
化简得 ![]() 为所求动圆圆心的轨迹方程。
为所求动圆圆心的轨迹方程。
解法二:由解法一得到![]() ,这说明P点是到两个定点O (0,0),A ( 4,0)的距离的差的绝对值都是常数1。(1 < 4)的点其轨迹是以O点A点为焦点,对称中心为
,这说明P点是到两个定点O (0,0),A ( 4,0)的距离的差的绝对值都是常数1。(1 < 4)的点其轨迹是以O点A点为焦点,对称中心为
O′(2,0),对称点为坐标轴 Ⅲ 2a = 1 2c = 4的双曲线。
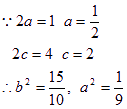
∴ 轨迹方程为 ![]()
解析:
动圆的定圆相切分外切、内切两种情况,若两圆外切,则圆心距等于两圆半径之和,若两圆内切,则圆心距等于两圆半径之差,动点满足的几何条件找到了,轨迹方程可求。本题对动点满足的几何关系分析得出符合圆锥曲线的定义,故而用解法二更为简捷些。

练习册系列答案
相关题目
 已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|
已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足|PQ|=|PA|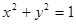 ,
,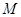 为抛物线
为抛物线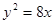 的焦点,
的焦点,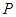 为⊙O外一点,由
为⊙O外一点,由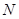 点,且
点,且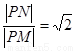
 抛物线
抛物线