题目内容
已知点M(0,-1),F(0,1),过点M的直线l与曲线y= x3-4x+4在x=2处的切线平行。
x3-4x+4在x=2处的切线平行。
(1)求直线l的方程;
(2)求以点F为焦点,l为准线的抛物线C的方程。
 x3-4x+4在x=2处的切线平行。
x3-4x+4在x=2处的切线平行。(1)求直线l的方程;
(2)求以点F为焦点,l为准线的抛物线C的方程。
解:(1)因为f′(2)=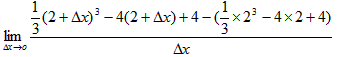 =0,
=0,
所以直线l的斜率为0,所以直线l的方程为y=-1;
(2)因为抛物线以点F(0,1)为焦点,直线y=-1为准线,
设抛物线的方程为x2=2py,
则 ,p=2,
,p=2,
故抛物线C的方程为x2=4y。
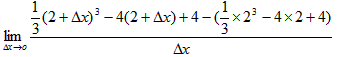 =0,
=0,所以直线l的斜率为0,所以直线l的方程为y=-1;
(2)因为抛物线以点F(0,1)为焦点,直线y=-1为准线,
设抛物线的方程为x2=2py,
则
 ,p=2,
,p=2,故抛物线C的方程为x2=4y。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目