题目内容
已知定义在R上的函数f(x)满足f(x)>0且对任意的x1,x2∈R,都有f(x1+x2)=f(x1)•f(x2)-2,且f(1)=2,则f(2)=______,若令f(x1)=a,f(x2)=b且f(x1+x2)=a+b,则a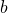 的取值范围是______.
的取值范围是______.
解:∵对任意的x1、x2∈R,都有f(x1+x2)=f(x1)•f(x2)-2,
∴令x1=x2=1,可得f(1+1)=f(1)+f(1)-2
结合f(1)=2,得f(2)=2f(1)-2=2×2-2=2;
∵f(x1)=a,f(x2)=b且f(x1+x2)=a+b,
∴结合f(x1+x2)=f(x1)•f(x2)-2,得ab-2=a+b
∵f(x1)=a,f(x2)=b均为正数
∴ab-2=a+b≥2 ,当且仅当a=b时等号成立
,当且仅当a=b时等号成立
即( )2-2
)2-2 -2≥0,解之得
-2≥0,解之得 ≤1-
≤1- 或
或 ≥1+
≥1+
结合 为正数,可得
为正数,可得 ≥1+
≥1+ ,所以ab≥(1+
,所以ab≥(1+ )2=4+2
)2=4+2
即a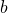 的取值范围是[4+2
的取值范围是[4+2 ,+∞)
,+∞)
故答案为:2,[4+2 ,+∞)
,+∞)
分析:对已知等式令x1=x2=1,可得f(1+1)=f(1)+f(1)-2,即f(2)=2f(1)-2=2×2-2=2;若f(x1)=a,f(x2)=b且f(x1+x2)=a+b,利用已知等式化简可得ab-2=a+b,结合基本不等式变形得到ab-2≥2 ,解关于
,解关于 的不等式得到
的不等式得到 ≥1+
≥1+ (舍负),从而得到ab的取值范围.
(舍负),从而得到ab的取值范围.
点评:本题给出特殊的抽象函数,求特殊的函数值并讨论ab的取值范围.着重考查了抽象函数的处理和基本不等式求最值等知识,属于中档题.
∴令x1=x2=1,可得f(1+1)=f(1)+f(1)-2
结合f(1)=2,得f(2)=2f(1)-2=2×2-2=2;
∵f(x1)=a,f(x2)=b且f(x1+x2)=a+b,
∴结合f(x1+x2)=f(x1)•f(x2)-2,得ab-2=a+b
∵f(x1)=a,f(x2)=b均为正数
∴ab-2=a+b≥2
 ,当且仅当a=b时等号成立
,当且仅当a=b时等号成立即(
 )2-2
)2-2 -2≥0,解之得
-2≥0,解之得 ≤1-
≤1- 或
或 ≥1+
≥1+
结合
 为正数,可得
为正数,可得 ≥1+
≥1+ ,所以ab≥(1+
,所以ab≥(1+ )2=4+2
)2=4+2
即a
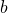 的取值范围是[4+2
的取值范围是[4+2 ,+∞)
,+∞)故答案为:2,[4+2
 ,+∞)
,+∞)分析:对已知等式令x1=x2=1,可得f(1+1)=f(1)+f(1)-2,即f(2)=2f(1)-2=2×2-2=2;若f(x1)=a,f(x2)=b且f(x1+x2)=a+b,利用已知等式化简可得ab-2=a+b,结合基本不等式变形得到ab-2≥2
 ,解关于
,解关于 的不等式得到
的不等式得到 ≥1+
≥1+ (舍负),从而得到ab的取值范围.
(舍负),从而得到ab的取值范围.点评:本题给出特殊的抽象函数,求特殊的函数值并讨论ab的取值范围.着重考查了抽象函数的处理和基本不等式求最值等知识,属于中档题.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |